题目内容
已知函数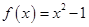 ,设曲线
,设曲线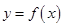 在点
在点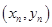 处的切线与
处的切线与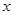 轴的交点为
轴的交点为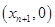 ,其中
,其中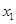 为正实数.
为正实数.
(1)用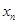 表示
表示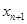 ;
;
(2)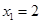 ,若
,若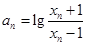 ,试证明数列
,试证明数列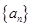 为等比数列,并求数列
为等比数列,并求数列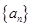 的通项公式;
的通项公式;
(3)若数列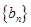 的前
的前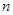 项和
项和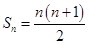 ,记数列
,记数列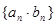 的前
的前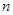 项和
项和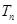 ,求
,求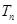 .
.
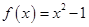 ,设曲线
,设曲线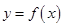 在点
在点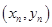 处的切线与
处的切线与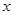 轴的交点为
轴的交点为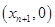 ,其中
,其中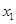 为正实数.
为正实数.(1)用
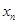 表示
表示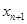 ;
;(2)
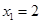 ,若
,若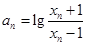 ,试证明数列
,试证明数列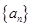 为等比数列,并求数列
为等比数列,并求数列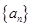 的通项公式;
的通项公式;(3)若数列
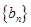 的前
的前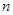 项和
项和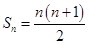 ,记数列
,记数列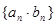 的前
的前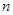 项和
项和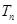 ,求
,求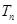 .
.(1)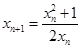 ;(2)证明见解析,
;(2)证明见解析,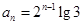 ;(3)
;(3)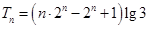 .
.
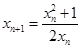 ;(2)证明见解析,
;(2)证明见解析,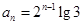 ;(3)
;(3)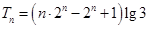 .
.试题分析:(1)直接利用导数得出切线斜率,写出点
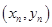 处切线方程,在切线方程中令
处切线方程,在切线方程中令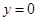 ,就可求出切线与
,就可求出切线与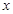 轴交点的横坐标即
轴交点的横坐标即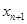 ;(2)要证明数列
;(2)要证明数列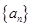 为等比数列,关键是找到
为等比数列,关键是找到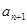 与
与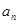 的关系,按题设,它们由
的关系,按题设,它们由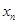 联系起来,
联系起来,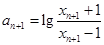 ,把
,把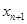 用(1)中的结论
用(1)中的结论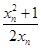 代换,变为
代换,变为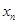 的式子,它应该与
的式子,它应该与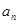 是有联系的,由此就可得出结论;(3)按照要求,首先求出数列
是有联系的,由此就可得出结论;(3)按照要求,首先求出数列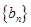 的通项公式,当然要利用
的通项公式,当然要利用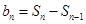 (
(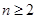 ),
),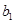 直接等于
直接等于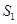 ,数列
,数列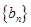 实际上是一个等差数列,那么数列
实际上是一个等差数列,那么数列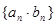 就是由一个等差数列和一个等比数列的对应项相乘得到的新数列,其前
就是由一个等差数列和一个等比数列的对应项相乘得到的新数列,其前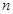 项的求法是乘公比错位相减法,即
项的求法是乘公比错位相减法,即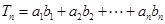 ,记等比数列
,记等比数列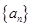 的公比是
的公比是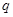 ,则有
,则有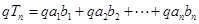
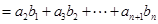 ,两式相减,即
,两式相减,即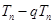 ,这个和是容易求得的.
,这个和是容易求得的.试题解析:(1)由题可得
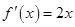 ,所以在曲线上点
,所以在曲线上点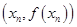 处的切线方程为
处的切线方程为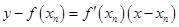 ,即
,即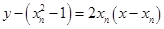
令
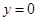 ,得
,得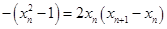 ,即
,即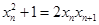
由题意得
 ,所以
,所以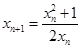 5′
5′(2)因为
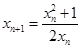 ,所以
,所以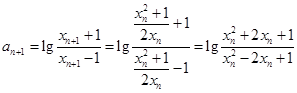
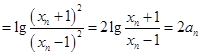 即
即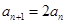 ,
,所以数列
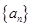 为等比数列故
为等比数列故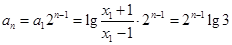 10′
10′(3)当
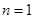 时,
时,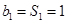 ,当
,当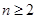 时,
时,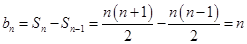
所以数列
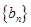 的通项公式为
的通项公式为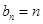 ,故数列
,故数列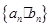 的通项公式为
的通项公式为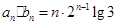
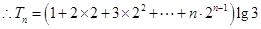 ①
①①
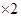 的
的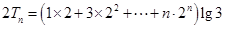 ②
②①
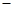 ②得
②得
故
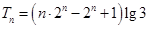 16′
16′
练习册系列答案
相关题目
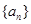 满足
满足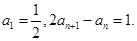

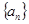 为等比数列,
为等比数列,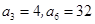 ,则
,则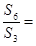 .
.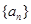 的第
的第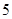 项是二项式
项是二项式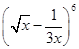 展开式的常数项,则
展开式的常数项,则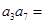 .
.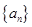 中,若
中,若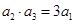 ,则
,则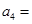 .
.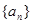 中,
中,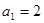 ,
,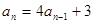 (
(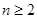 ),则数列
),则数列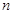 项和
项和 .
.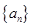 满足
满足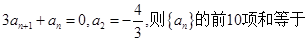 ( )
( )



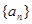 中,首项为3,前3项和为21,则
中,首项为3,前3项和为21,则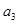 等于( )
等于( ) ,-1)
,-1)