题目内容
【题目】已知函数![]() .
.
(1)求函数的定义域;
(2)判断函数的奇偶性,并证明你的结论;
(3)在函数![]() 图像上是否存在两个不同的点
图像上是否存在两个不同的点![]() ,使直线
,使直线![]() 垂直
垂直![]() 轴,若存在,求出
轴,若存在,求出![]() 两点坐标;若不存在,说明理由.
两点坐标;若不存在,说明理由.
【答案】(1) 函数![]() 的定义域为
的定义域为![]() ;(2)见解析;(3)见解析.
;(2)见解析;(3)见解析.
【解析】试题分析:(1)根据函数的解析式有意义的原则,结合对数的真数部分必须大于0,构造关于x的不等式组,解不等式组,即可得到答案;
(2)根据函数奇偶性的定义,利用对数的运算性质,判断f(﹣x)与f(x)的关系,即可得到函数f(x)的奇偶性;
(3) 假设函数![]() 图象上存在两点A(
图象上存在两点A(![]() ,
,![]() ),
),![]() , 使直线
, 使直线![]() 垂直
垂直![]() 轴,则
轴,则![]() ,
,
经推理不成立,故不存在.
试题解析:
(1) 由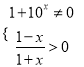
![]() ,
,
∴ 函数![]() 的定义域为
的定义域为![]()
(2) ∵f (-x)= ![]() + lg
+ lg![]() =
=![]() – lg
– lg![]() =-f (x),
=-f (x),
∴ f (x)是奇函数
(3)假设函数![]() 图象上存在两点A(
图象上存在两点A(![]() ,
,![]() ),
),![]() ,
,
使直线AB恰好与y轴垂直,其中![]() .
.
即当![]() 时,
时, ![]() , 不妨设
, 不妨设![]() ,
,![]()
于是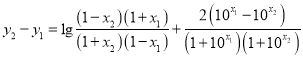
由![]()
![]()
![]()
又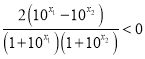
![]() , ∴
, ∴![]() , 与
, 与![]() =
=![]() 矛盾.
矛盾.
故函数![]() 图象上不存在两个不同的点A、B,使直线AB垂直y轴.
图象上不存在两个不同的点A、B,使直线AB垂直y轴.

练习册系列答案
 培优三好生系列答案
培优三好生系列答案 优化作业上海科技文献出版社系列答案
优化作业上海科技文献出版社系列答案
相关题目