题目内容
【题目】若抛物线y2=2px（p＞0）上一点到焦点和抛物线对称轴的距离分别为10和6，则抛物线方程为（ ）
A.y2=4x
B.y2=36x
C.y2=4x或y2=36x
D.y2=8x或y2=32x
【答案】C
【解析】解：∵抛物线y2=2px（p＞0）上一点到的对称轴的距离6，
∴设该点为P，则P的坐标为（x0，±6）
∵P到抛物线的焦点F（ 
，0）的距离为10
∴由抛物线的定义，得x0+ =10…（1）
∵点P是抛物线上的点，
∴2px0=36…（2）
由（1）（2）联立，解得p=2，x0=2或p=18，x0=1
则抛物线方程为y2=4x或y2=36x．
故选：C．
由抛物线上点P到的对称轴的距离6，设P的坐标为（x0，±6）．根据点P坐标适合抛物线方程及点P到焦点的距离为10，联列方程组，解之可得p与x0的值，从而得到本题的答案．
练习册系列答案
相关题目
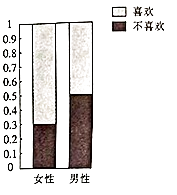
【题目】为了调查喜欢旅游是否与性别有关，调查人员就“是否喜欢旅游”这个问题，在火车站分别随机调研了50名女性和50名男性，根据调研结果得到如图所示的等高条形图
（1）完成下列2×2列联表：
喜欢旅游 | 不喜欢旅游 | 合计 | |
女性 | |||
男性 | |||
合计 |
（2）能否在犯错率不超过0.025的前提下认为“喜欢旅游与性别有关” 附：
P（K2≥k0） | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
k0 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
（参考公式：K2= 
，其中n=a+b+c+d）
