题目内容
从原点O引直线交直线2x+4y-1=0于点M,P为OM上一点,已知OP·OM=1,求P点所在曲线的极坐标方程.
ρ=2cosθ+4sinθ
【解析】以O为极点,x轴正方向为极轴建立极坐标系,直线方程化为
2ρcosθ+4ρsinθ-1=0,
设M(ρ0,θ0),P(ρ,θ),则2ρ0cosθ0+4ρ0sinθ0-1=0.
又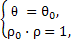
知
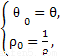
代入得:2
cosθ+4sinθ-1=0,∴ρ=2cosθ+4sinθ.
练习册系列答案
相关题目
题目内容
从原点O引直线交直线2x+4y-1=0于点M,P为OM上一点,已知OP·OM=1,求P点所在曲线的极坐标方程.
ρ=2cosθ+4sinθ
【解析】以O为极点,x轴正方向为极轴建立极坐标系,直线方程化为
2ρcosθ+4ρsinθ-1=0,
设M(ρ0,θ0),P(ρ,θ),则2ρ0cosθ0+4ρ0sinθ0-1=0.
又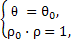知
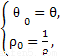
代入得:2cosθ+4sinθ-1=0,∴ρ=2cosθ+4sinθ.
