题目内容
19.已知f′(x)是定义在R上的函数y=f(x)的导函数,且f(x)<f′(x),则a=$\frac{1}{2}$f(ln2),b=$\frac{1}{e}$f(1),c=f(0)的大小关系为( )| A. | a<b<c | B. | b<a<c | C. | c<b<a | D. | c<a<b |
分析 构造函数g(x)=$\frac{f(x)}{{e}^{x}}$,利用导数可判断g(x)的单调性,由单调性可得a=g(ln2)与c=g(0)、b=g(1)的大小关系,即可得到答案.
解答 解:令g(x)=$\frac{f(x)}{{e}^{x}}$,则g′(x)=$\frac{f′(x)•{e}^{x}-f(x)•{e}^{x}}{{e}^{2x}}$=$\frac{f′(x)-f(x)}{{e}^{x}}$,
因为对任意x∈R都有f′(x)>f(x),
所以g′(x)>0,即g(x)在R上单调递增,
又a=$\frac{f(ln2)}{{e}^{ln2}}$=g(ln2),b=$\frac{f(1)}{e}$=g(1),c=$\frac{f(0)}{{e}^{0}}$=g(0),
由0<ln2<1,可得g(0)<g(ln2)<g(1),
即c<a<b.
故选:D.
点评 本题考查导数的运用:求单调性,考查导数的运算性质的运用,以及单调性的运用:比较大小,属于中档题.

练习册系列答案
相关题目
14.设logbN<logaN<0,N>1,且a+b=1,则必有( )
| A. | 1<a<b | B. | a<b<1 | C. | 1<b<a | D. | b<a<1 |
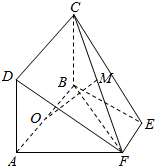 如图,在四边形ABEF中,AF⊥FB,O为AB的中点,矩形ABCD所在的平面垂直于平面ABEF.
如图,在四边形ABEF中,AF⊥FB,O为AB的中点,矩形ABCD所在的平面垂直于平面ABEF.