题目内容
4.等比数列{an}同时满足下列条件:①a1+a6=33,②a3a4=32,③三个数4a2,2a3,a4依次成等差数列.(1)求数列{an}的通项公式;
(2)记bn=$\frac{n}{{a}_{n}}$,求数列{bn}的前n项和Tn.
分析 (1)通过设等比数列{an}的公比为q,利用4a3=4a2+a4计算可知q=2,通过a1+a6=33可知a1=1,从而可知数列{an}是以1为首项、2为公比的等比数列,计算即得结论;
(2)通过(1)可知bn=$\frac{n}{{2}^{n-1}}$,利用错位相减法计算即得结论.
解答 解:(1)设等比数列{an}的公比为q,
∵三个数4a2,2a3,a4依次成等差数列,
∴4a3=4a2+a4,即4a1q2=4a1q+a1q3,
整理得:0=4+q2-4q,
解得:q=2,
又∵a1+a6=33,即a1+25a1=33,
解得:a1=1,
∴数列{an}是以1为首项、2为公比的等比数列,
∴an=2n-1;
(2)由(1)可知bn=$\frac{n}{{a}_{n}}$=$\frac{n}{{2}^{n-1}}$,
∴Tn=$1•\frac{1}{{2}^{0}}$+2•$\frac{1}{2}$+…+n•$\frac{1}{{2}^{n-1}}$,
∴$\frac{1}{2}$Tn=1•$\frac{1}{2}$+2•$\frac{1}{{2}^{2}}$+…+n•$\frac{1}{{2}^{n}}$,
两式相减得:$\frac{1}{2}$Tn=1+$\frac{1}{2}$+$\frac{1}{{2}^{2}}$+…+$\frac{1}{{2}^{n-1}}$-n•$\frac{1}{{2}^{n}}$
=$\frac{1-\frac{1}{{2}^{n}}}{1-\frac{1}{2}}$-n•$\frac{1}{{2}^{n}}$
=2-$\frac{n+2}{{2}^{n}}$,
∴Tn=2(2-$\frac{n+2}{{2}^{n}}$)=4-$\frac{n+2}{{2}^{n-1}}$.
点评 本题考查数列的通项及前n项和,考查运算求解能力,考查错位相减法,注意解题方法的积累,属于中档题.

 阅读快车系列答案
阅读快车系列答案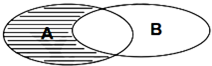 设集合A={x|x2+2x-3<0},B={x|x<0},则如图中阴影部分表示的集合为( )
设集合A={x|x2+2x-3<0},B={x|x<0},则如图中阴影部分表示的集合为( )| A. | {x|0≤x<3} | B. | {x|0≤x<1} | C. | {x|-3<x<0} | D. | {x|0<x<1} |
| A. | a<b<c | B. | b<a<c | C. | c<b<a | D. | c<a<b |