题目内容
11．如图，P是正方体ABCD-A′B′C′D′的面ABCD上任意一点，试在面ABCD内过点P作直线l，使l⊥PC′．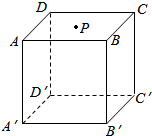
分析 连接PC，在面ABCD内过点P作直线l，使l⊥PC，利用线面垂直的判定与性质，即可得出结论．
解答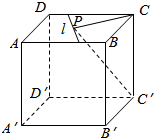 
解：连接PC，在面ABCD内过点P作直线l，使l⊥PC，则
∵l⊥PC，l⊥C′C，PC∩C′C=C，
∴l⊥平面PC′C，
∵PC′?平面PC′C，
∴l⊥PC′．
点评 本题考查线面垂直的判定与性质，考查学生的作图能力，比较基础．
练习册系列答案
超能学典应用题题卡系列答案
相关题目
1．已知变量x，y满足约束条件$\left\{\begin{array}{l}{x+y≥2}\\{x-y≤2}\\{0≤y≤3}\end{array}\right.$，则目标函数2x-y的最大值是7．
19．已知f′（x）是定义在R上的函数y=f（x）的导函数，且f（x）＜f′（x），则a=$\frac{1}{2}$f（ln2），b=$\frac{1}{e}$f（1），c=f（0）的大小关系为（ ）
| A． | a＜b＜c | B． | b＜a＜c | C． | c＜b＜a | D． | c＜a＜b |
8．同时满足性质：“①对任意的x∈R，f（x+$\frac{π}{2}$）=-f（x）恒成立；②对任意的x∈R，f（$\frac{π}{3}$+x）=f（$\frac{π}{3}$-x）恒成立；③在[-$\frac{π}{6}$，$\frac{π}{3}$]上是增函数．”的函数可以是（ ）
| A． | f（x）=sin（2x+$\frac{π}{6}$） | B． | f（x）=sin（2x-$\frac{π}{6}$） | C． | f（x）=cos（2x+$\frac{π}{6}$） | D． | f（x）=cos（2x-$\frac{π}{6}$） |