题目内容
9.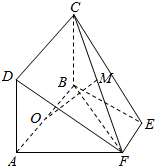 如图,在四边形ABEF中,AF⊥FB,O为AB的中点,矩形ABCD所在的平面垂直于平面ABEF.
如图,在四边形ABEF中,AF⊥FB,O为AB的中点,矩形ABCD所在的平面垂直于平面ABEF.(1)求证:AF⊥平面CBF;
(2)设FC的中点为M,求证:OM∥平面DAF.
分析 (1)欲证AF⊥平面CBF,根据直线与平面垂直的判定定理可知只需证AF与平面CBF内两相交直线垂直,而AF⊥CB,AF⊥BF,BF∩BC=B,满足定理条件;
(2)欲证OM∥平面DAF,根据直线与平面平行的判定定理可知只需证OM/与平面DAF内一直线平行,设DF的中点为N,OM∥AN又AN?平面DAF,OM?平面DAF,满足定理条件.
解答 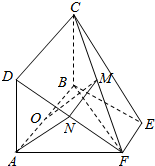 (1)证明:∵平面ABCD⊥平面ABEF,CB⊥AB,平面ABCD∩平面ABEF=AB,
(1)证明:∵平面ABCD⊥平面ABEF,CB⊥AB,平面ABCD∩平面ABEF=AB,
∴CB⊥平面ABEF,
∵AF?平面ABEF,
∴AF⊥CB,
又AF⊥BF,且BF∩BC=B,BF、BC?平面CB,
∴AF⊥平面CBF.
(2)证明:设DF的中点为N,则MN$\stackrel{∥}{=}$$\frac{1}{2}$CD,又AO$\stackrel{∥}{=}$$\frac{1}{2}$CD,则MN$\stackrel{∥}{=}$AO,
∴MNAO为平行四边形,
∴OM∥AN,
又AN?平面DAF,OM?平面DAF,
∴OM∥平面DAF.
点评 本题主要考查了直线与平面垂直的判定,以及直线与平面平行的判定,考查空间想象能力、运算能力和推理论证能力,属于中档题.

练习册系列答案
相关题目
14.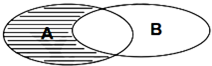 设集合A={x|x2+2x-3<0},B={x|x<0},则如图中阴影部分表示的集合为( )
设集合A={x|x2+2x-3<0},B={x|x<0},则如图中阴影部分表示的集合为( )
 设集合A={x|x2+2x-3<0},B={x|x<0},则如图中阴影部分表示的集合为( )
设集合A={x|x2+2x-3<0},B={x|x<0},则如图中阴影部分表示的集合为( )| A. | {x|0≤x<3} | B. | {x|0≤x<1} | C. | {x|-3<x<0} | D. | {x|0<x<1} |
1.已知变量x,y满足约束条件$\left\{\begin{array}{l}{x+y≥2}\\{x-y≤2}\\{0≤y≤3}\end{array}\right.$,则目标函数2x-y的最大值是7.
19.已知f′(x)是定义在R上的函数y=f(x)的导函数,且f(x)<f′(x),则a=$\frac{1}{2}$f(ln2),b=$\frac{1}{e}$f(1),c=f(0)的大小关系为( )
| A. | a<b<c | B. | b<a<c | C. | c<b<a | D. | c<a<b |