题目内容
直线y=一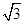 x与椭圆C:
x与椭圆C: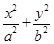 =1(a>b>0)交于A、B两点,以线段AB为直径的圆恰好经过椭圆的右焦点,则椭圆C的离心率为.
=1(a>b>0)交于A、B两点,以线段AB为直径的圆恰好经过椭圆的右焦点,则椭圆C的离心率为.
A.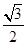 B.
B.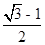 C.
C.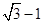 D.4-2
D.4-2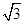
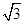 x与椭圆C:
x与椭圆C: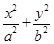 =1(a>b>0)交于A、B两点,以线段AB为直径的圆恰好经过椭圆的右焦点,则椭圆C的离心率为.
=1(a>b>0)交于A、B两点,以线段AB为直径的圆恰好经过椭圆的右焦点,则椭圆C的离心率为.A.
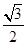 B.
B.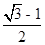 C.
C.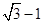 D.4-2
D.4-2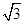
C
由 得:
得: 所以
所以 则
则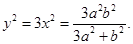 根据椭圆得
根据椭圆得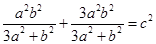 ;所以
;所以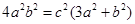
 整理得:
整理得: ,所以
,所以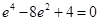 ;解得
;解得
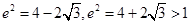 (舍去)。所以
(舍去)。所以 故选C
故选C
 得:
得: 所以
所以 则
则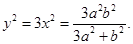 根据椭圆得
根据椭圆得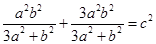 ;所以
;所以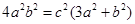
 整理得:
整理得: ,所以
,所以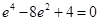 ;解得
;解得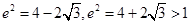 (舍去)。所以
(舍去)。所以 故选C
故选C
练习册系列答案
相关题目
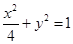 的焦点为
的焦点为 、
、 ,在长轴
,在长轴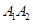 上任取一点
上任取一点 ,过
,过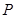 ,则使得
,则使得 的
的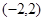




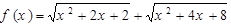 的最小值为( )
的最小值为( )


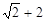
 的上焦点是
的上焦点是 ,过点P(3,4)和
,过点P(3,4)和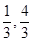 ).
). 内有一点P
内有一点P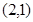 ,以P为中点作弦MN,则直线MN的方程是( )
,以P为中点作弦MN,则直线MN的方程是( )



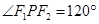 ,则椭圆的离心率的取值范围是( )
,则椭圆的离心率的取值范围是( )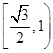
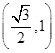
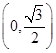
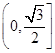
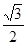 ,且G上一点到G的两个焦点的距离之和为12,则椭圆G的方程为 __
,且G上一点到G的两个焦点的距离之和为12,则椭圆G的方程为 __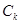 的方程:
的方程: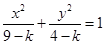 .
.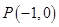 ,是否存在曲线
,是否存在曲线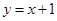 于
于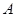 、
、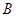 两点,使得
两点,使得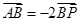 ?若存在,求出
?若存在,求出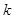 的值;若不存在,说明理由;
的值;若不存在,说明理由;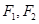 分别为椭圆
分别为椭圆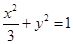 的焦点,点
的焦点,点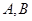 在椭圆上,若
在椭圆上,若 ;则点
;则点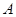
 的坐标是 _________
的坐标是 _________