ΧβΡΩΡΎ»ί
ΓΨΧβΡΩΓΩ‘Ύ °Ψ≈¥σΜα“ι…œΘ§Β≥÷–―κΟς»Ζ«ΩΒςΓΑΦα≥÷ΖΩΉ” «”Οά¥ΉΓΒΡΓ≠Γ≠Γ±Θ§ΒΟΒΫΝΥΗςΦΕ’ΰΗ°ΦΑœύΙΊΒΞΈΜΒΡΜΐΦΪœλ”Π.‘ΎΦΟΡΰΘ§ΥφΉ≈ΦΟΡΰ“Μ÷–…ΐ―߬ ΒΡΫΎΫΎ≈ …ΐΘ§±±Κΰ–Θ«χΗΫΫϋΒΡΖΩΦέ“≤‘Ύ≤ΜΕœ≈ …ΐΘ§ΈΣ¬ζΉψΙψ¥σ»ΥΟώ»Κ÷ΎΒΡΙΚΖΩ–η«σΘ§“Μ÷–±±ΚΰΗΫΫϋΒΡ“ΜΗω¬Ξ≈ΧΩΣ≈ΧΦέ“―œόΕ®ΈΣΟΩΤΫΟΉ≤Μ≥§Ιΐ7«ß‘ΣΘ§ΟΩ≤ψΟΩΤΫΟΉΒΡΦέΗώ![]() Θ®«ß‘ΣΘ©”κ¬Ξ≤ψ
Θ®«ß‘ΣΘ©”κ¬Ξ≤ψ![]() ÷°ΦδΖϊΚœ“ΜΗωΕΰ¥ΈΚ· ΐΒΡ±δΜ·Ιφ¬…Θ§ΤΎ÷–“ΜΕΑΗΏ33≤ψΒΡΗΏ≤ψΉΓ’§ΉνΒΆœζ έΦέΈΣΒΉ≤ψΘ®“Μ¬ΞΘ©ΟΩΤΫΟΉ6«ß‘ΣΘ§ΉνΗΏΦέΈΣΒΎ20≤ψΟΩΤΫΟΉ7«ß‘Σ.
÷°ΦδΖϊΚœ“ΜΗωΕΰ¥ΈΚ· ΐΒΡ±δΜ·Ιφ¬…Θ§ΤΎ÷–“ΜΕΑΗΏ33≤ψΒΡΗΏ≤ψΉΓ’§ΉνΒΆœζ έΦέΈΣΒΉ≤ψΘ®“Μ¬ΞΘ©ΟΩΤΫΟΉ6«ß‘ΣΘ§ΉνΗΏΦέΈΣΒΎ20≤ψΟΩΤΫΟΉ7«ß‘Σ.
Θ®1Θ©ΗυΨί“‘…œ–≈œΔ–¥≥ω’βΗωΕΰ¥ΈΚ· ΐΒΡ±μ¥ο Ϋ![]() ΦΑΕ®“ε”ρ.
ΦΑΕ®“ε”ρ.
Θ®2Θ©Ρ≥ΒΞΈΜΩΦ¬«ΒΫ÷ΑΙΛΉ”≈°»Ξ“Μ÷–ΨΆ―ßΒΡ ΒΦ –η“ΣΘ§ΦΤΜ°Ά≈ΙΚΉΓΖΩΘ§ΨΓΝΠ’υ»ΓΆ≈ΙΚ”≈Μί’ΰ≤ΏΘ§»γΙϊΒΟΒΫΒΡ”≈Μί’ΰ≤Ώ «‘ΎΟΩΧΉΖΩΉήΦέΒΡΜυ¥Γ…œΦθ»Ξ20Θ®«ß‘ΣΘ©ΚσΘ§‘Ό“‘”ύΩνΒΡΨ≈Έε’έΫΪΫ®÷ΰΟφΜΐΈΣ95ΤΫΟΉΒΡΖΩ–Ά≥ω έΗχΗΟΒΞΈΜ÷ΑΙΛΘ§’≈Ρ≥ΚΆάνΡ≥Ζ÷±π―ΓΕ®ΝΥ1¬ΞΚΆ25¬ΞΘ§«κΡψΗυΨίΚ· ΐ–‘÷ Θ§±»Ϋœ’≈Ρ≥ΚΆάνΡ≥Υ≠ΜώΒΟΒΡ”≈ΜίΕνΕ»Ηϋ¥σ“Μ–©ΘΩ’β“Μ”≈ΜίΒΡΕνΕ»ΈΣΕύ…ΌΘ®«ß‘ΣΘ©ΘΩΘ®ΉΔΘΚΨ≈Έε’έ--Α¥‘≠ΦέΒΡ![]() ’έΈΣœ÷ΦέΘ©Θ®ΨΪ»ΖΒΫ0.001«ß‘ΣΘ©.
’έΈΣœ÷ΦέΘ©Θ®ΨΪ»ΖΒΫ0.001«ß‘ΣΘ©.
ΓΨ¥πΑΗΓΩΘ®1Θ©![]() Θ§Ε®“ε”ρΈΣΘΚ
Θ§Ε®“ε”ρΈΣΘΚ![]() ΘΜΘ®2Θ©άνΡ≥ΒΡ”≈ΜίΕνΕ»¥σ“Μ–©Θ§ΈΣ51921‘Σ.
ΘΜΘ®2Θ©άνΡ≥ΒΡ”≈ΜίΕνΕ»¥σ“Μ–©Θ§ΈΣ51921‘Σ.
ΓΨΫβΈωΓΩ
Θ®1Θ©ΗυΨίΕΰ¥ΈΚ· ΐ…ηΕΞΒψ Ϋ±μ¥ο ΫΘ§ΗυΨί![]() «σΫβΘΜ
«σΫβΘΜ
Θ®2Θ©–¥≥ω”≈ΜίΕνΕ»ΈΣ![]() ΫβΈω ΫΘ§
ΫβΈω ΫΘ§ ![]() Θ§
Θ§![]() Θ§Ζ÷±πΦΤΥψ’≈Ρ≥ΚΆάνΡ≥ΒΡ”≈ΜίΕνΕ»Φ¥Ω…ΒΟΫβ.
Θ§Ζ÷±πΦΤΥψ’≈Ρ≥ΚΆάνΡ≥ΒΡ”≈ΜίΕνΕ»Φ¥Ω…ΒΟΫβ.
Θ®1Θ©”…ΧβΟΩ≤ψΟΩΤΫΟΉΒΡΦέΗώ![]() Θ®«ß‘ΣΘ©”κ¬Ξ≤ψ
Θ®«ß‘ΣΘ©”κ¬Ξ≤ψ![]() ÷°ΦδΖϊΚœ“ΜΗωΕΰ¥ΈΚ· ΐΒΡ±δΜ·Ιφ¬…Θ§ΉνΗΏΦέΈΣΒΎ20≤ψΟΩΤΫΟΉ7«ß‘ΣΘ§
÷°ΦδΖϊΚœ“ΜΗωΕΰ¥ΈΚ· ΐΒΡ±δΜ·Ιφ¬…Θ§ΉνΗΏΦέΈΣΒΎ20≤ψΟΩΤΫΟΉ7«ß‘ΣΘ§
Ω……η![]() Θ§«“
Θ§«“![]() Θ§
Θ§
Υυ“‘![]() Θ§ΫβΒΟΘΚ
Θ§ΫβΒΟΘΚ![]()
Υυ“‘’βΗωΕΰ¥ΈΚ· ΐΒΡ±μ¥ο Ϋ![]() Φ¥ΘΚ
Φ¥ΘΚ
![]() Θ§Ε®“ε”ρΈΣΘΚ
Θ§Ε®“ε”ρΈΣΘΚ![]() ΘΜ
ΘΜ
Θ®2Θ©…η”≈ΜίΕνΕ»ΈΣ![]() Θ§ΗυΨί”≈ΜίΖΫΑΗΩ…ΒΟΘΚ
Θ§ΗυΨί”≈ΜίΖΫΑΗΩ…ΒΟΘΚ
![]() Θ§
Θ§![]() Θ§
Θ§
ΗυΨίΚ· ΐΫβΈω ΫΩ…ΒΟΘΚ![]() «“ΜΗωΩΣΩΎ≥·œ¬ΒΡΕΰ¥ΈΚ· ΐΘ§Ε‘≥Τ÷α
«“ΜΗωΩΣΩΎ≥·œ¬ΒΡΕΰ¥ΈΚ· ΐΘ§Ε‘≥Τ÷α![]() Θ§
Θ§
Υυ“‘![]() Θ§
Θ§
’≈Ρ≥ΒΡ”≈ΜίΕνΕ»ΘΚ![]()
άνΡ≥ΒΡ”≈ΜίΕνΕ»ΘΚ![]()
Υυ“‘άνΡ≥ΒΡ”≈ΜίΕνΕ»¥σ“Μ–©Θ§ΈΣ51921‘Σ.

ΓΨΧβΡΩΓΩ“―÷ΣΡ≥÷–―ßΗΏ»ΐΈΡΩΤΑύ―ß…ζΙ≤”–800»Υ≤ΈΦ” ΐ―ß”κΒΊάμΒΡ―ß“ΒΥ°ΤΫ≤β ‘Θ§¥”÷–ΥφΜζ≥ι»Γ100»ΥΒΡ ΐ―ß”κΒΊάμΒΡ―ß“ΒΥ°ΤΫ≤β ‘≥…Φ®»γœ¬±μΘΚ
»Υ ΐ | ΐ―ß | |||
”≈–ψ | ΝΦΚΟ | ΦΑΗώ | ||
ΒΊάμ | ”≈–ψ | 7 | 20 | 5 |
ΝΦΚΟ | 9 | 18 | 6 | |
ΦΑΗώ | a | 4 | b | |
≥…Φ®Ζ÷ΈΣ”≈–ψΓΔΝΦΚΟΓΔΦΑΗώ»ΐΗωΒ»ΦΕΘ§ΚαœρΓΔΉίœρΖ÷±π±μ ΨΒΊάμ≥…Φ®”κ ΐ―ß≥…Φ®άΐ»γΘΚ±μ Ψ ΐ―ß≥…Φ®ΈΣΝΦΚΟΒΡΙ≤”–20ΘΪ18ΘΪ4ΘΫ42(»Υ)Θ°
(Δώ)»τ‘ΎΗΟ―υ±Ψ÷–Θ§ ΐ―ß≥…Φ®”≈–ψ¬ ΈΣ30%Θ§«σaΘ§bΒΡ÷ΒΘΜ
(Δρ)“―÷ΣaΓί10Θ§bΓί8Θ§άϊ”Ο―υ±Ψ ΐΨίΘ§«σ ΐ―ß≥…Φ®ΈΣ”≈–ψΒΡ»Υ ΐ±»ΦΑΗώΒΡ»Υ ΐ…ΌΒΡΗ≈¬ Θ°
ΓΨΧβΡΩΓΩΡ≥ΒΊΒγ”Α‘ΚΈΣΝΥΝΥΫβΒ±ΒΊ”ΑΟ‘Ε‘Ωλ“Σ…œ”≥ΒΡ“Μ≤ΩΒγ”ΑΒΡΤ±ΦέΒΡΩ¥Ζ®Θ§Ϋχ––ΝΥ“Μ¥ΈΒς―–Θ§ΒΟΒΫΝΥΤ±Φέx(ΒΞΈΜΘΚ‘Σ)”κΩ ΆϊΙέ”Α»Υ ΐy(ΒΞΈΜΘΚΆρ»Υ)ΒΡΫαΙϊ»γœ¬±μΘΚ
x(ΒΞΈΜΘΚ‘Σ) | 30 | 40 | 50 | 60 |
y(ΒΞΈΜΘΚΆρ»Υ) | 4.5 | 4 | 3 | 2.5 |
(1)»τy”κxΨΏ”–Ϋœ«ΩΒΡœύΙΊΙΊœΒΘ§ ‘Ζ÷Έωy”κx÷°Φδ «’ΐœύΙΊΜΙ «ΗΚœύΙΊΘΜ
(2)«κΗυΨί…œ±μΧαΙ©ΒΡ ΐΨίΘ§”ΟΉν–ΓΕΰ≥ΥΖ®«σ≥ωyΙΊ”ΎxΒΡœΏ–‘ΜΊΙιΖΫ≥ΧΘΜ
(3)ΗυΨί(2)÷–«σ≥ωΒΡœΏ–‘ΜΊΙιΖΫ≥ΧΘ§‘Λ≤βΤ±ΦέΕ®ΈΣΕύ…Ό‘Σ ±Θ§ΡήΜώΒΟΉν¥σΤ±ΖΩ ’»κΘ°
≤ΈΩΦΙΪ ΫΘΚ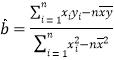 Θ§
Θ§![]() .
.