Question

【题目】已知f(x)＝x2－2ax＋2(a∈R)，当x∈[－1，＋∞)时，恒成立，则a的取值范围是_________．

Answer 1

【答案】.

【解析】试题分析：g(x)＝x2－2ax＋2－a，根据对称轴与定义区间位置关系分类讨论：当时， ；当时， ；解不等式，再求并集得a的取值范围．

试题解析：解：法一：f(x)＝(x－a)2＋2－a2，此二次函数图象的对称轴为x＝a.

①当a∈(－∞，－1)时，f(x)在[－1，＋∞)上单调递增，

f(x)min＝f(－1)＝2a＋3.

要使f(x)≥a恒成立，只需f(x)min≥a，

即2a＋3≥a，解得－3≤a＜－1；

②当a∈[－1，＋∞，)时，f(x)min＝f(a)＝2－a2，

由2－a2≥a，解得－1≤a≤1.

综上所述，所求a的取值范围为－3≤a≤1.

法二：令g(x)＝x2－2ax＋2－a，由已知，得

x2－2ax＋2－a≥0在[－1，＋∞)上恒成立，

即Δ＝4a2－4(2－a)≤0或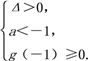

解得－3≤a≤1.