题目内容
(本小题满分14分)
已知椭圆的中心在原点,焦点在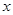 轴上,长轴长是短轴长的2倍,且经过点
轴上,长轴长是短轴长的2倍,且经过点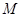 (2,1),平行于
(2,1),平行于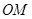 直线
直线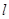 在
在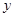 轴上的截距为
轴上的截距为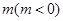 ,设直线
,设直线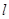 交椭圆于两个不同点
交椭圆于两个不同点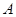 、
、 ,
,
(1)求椭圆方程;
(2)求证:对任意的 的允许值,
的允许值,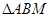 的内心在定直线
的内心在定直线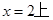 。
。
已知椭圆的中心在原点,焦点在
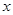 轴上,长轴长是短轴长的2倍,且经过点
轴上,长轴长是短轴长的2倍,且经过点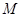 (2,1),平行于
(2,1),平行于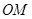 直线
直线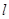 在
在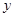 轴上的截距为
轴上的截距为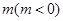 ,设直线
,设直线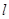 交椭圆于两个不同点
交椭圆于两个不同点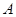 、
、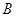 ,
,
(1)求椭圆方程;
(2)求证:对任意的
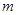 的允许值,
的允许值,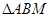 的内心在定直线
的内心在定直线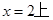 。
。(1)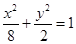 (2)直线
(2)直线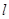 为
为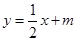 ,由
,由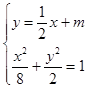 得
得
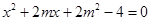 ,
,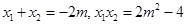 设直线
设直线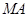 、
、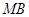 的斜率分别为
的斜率分别为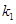 、
、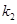 ,
,
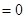 所以,
所以,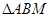 的角平分线垂直
的角平分线垂直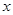 轴,因此,内心的横坐标等于点
轴,因此,内心的横坐标等于点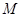 的横坐标,则对任意的
的横坐标,则对任意的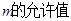 ,
,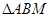 的内心在定直线
的内心在定直线 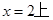
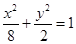 (2)直线
(2)直线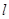 为
为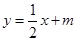 ,由
,由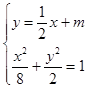 得
得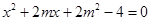 ,
,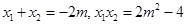 设直线
设直线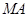 、
、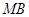 的斜率分别为
的斜率分别为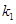 、
、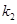 ,
,
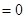 所以,
所以,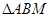 的角平分线垂直
的角平分线垂直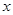 轴,因此,内心的横坐标等于点
轴,因此,内心的横坐标等于点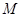 的横坐标,则对任意的
的横坐标,则对任意的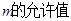 ,
,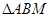 的内心在定直线
的内心在定直线 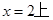
试题分析:(1)设椭圆方程为
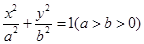
则
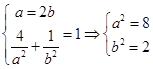 所以椭圆方程为
所以椭圆方程为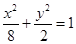 …… 5分
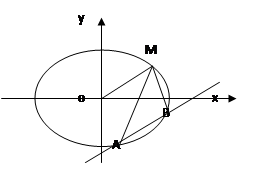
…… 5分(2)如图,因为直线
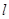 平行于
平行于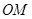 ,且在
,且在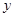 轴上的截距为
轴上的截距为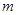 ,又
,又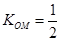 ,所以,直线
,所以,直线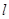 的方程为
的方程为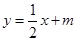 , 由
, 由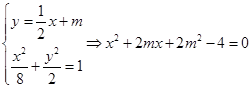 ,
,设
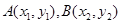 ,则
,则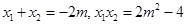 ,…………8分
,…………8分设直线
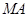 、
、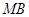 的斜率分别为
的斜率分别为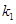 、
、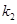 ,则
,则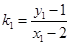 ,
,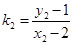
故
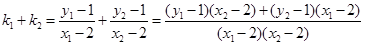 =
=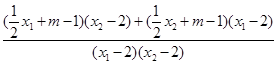 =
=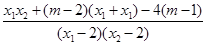
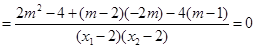 ……………12分
……………12分 故
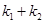 =0, 所以,
=0, 所以,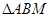 的角平分线垂直
的角平分线垂直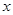 轴,因此,内心的横坐标等于点
轴,因此,内心的横坐标等于点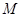 的横坐标,则对任意的
的横坐标,则对任意的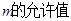 ,
,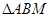 的内心在定直线
的内心在定直线 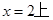 ……14
……14点评:直线与椭圆相交,利用韦达定理设而不求是常用的思路,本题要证内心在定直线上转化为两边关于该直线对称,进而与斜率联系起来

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
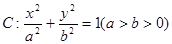 ,
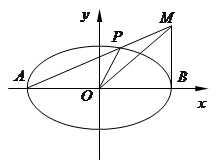
,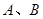 是长轴的左、右端点,动点
是长轴的左、右端点,动点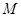 满足
满足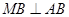 ,联结
,联结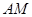 ,交椭圆于点
,交椭圆于点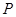 .
. 
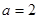 ,
,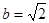 时,设
时,设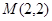 ,求
,求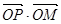 的值;
的值;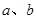 满足的条件?并说明理由;
满足的条件?并说明理由;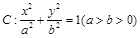 ,直线l为圆
,直线l为圆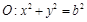 的一条切线,且经过椭圆C的右焦点,直线l的倾斜角为
的一条切线,且经过椭圆C的右焦点,直线l的倾斜角为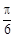 ,记椭圆C的离心率为e.
,记椭圆C的离心率为e.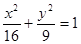 的焦距是 ,焦点坐标为
的焦距是 ,焦点坐标为 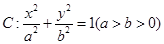 的离心率为
的离心率为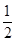 ,且过点
,且过点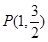 ,
,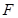 为其右焦点.
为其右焦点.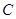 的方程;
的方程; 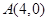 的直线
的直线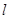 与椭圆相交于
与椭圆相交于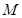 、
、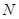 两点(点
两点(点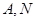 两点之间),若
两点之间),若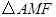 与
与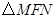 的面积相等,试求直线
的面积相等,试求直线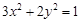 的焦点坐标是( )
的焦点坐标是( ) )、(0,
)、(0, )
)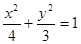 的左、右焦点分别为F1、F2,过椭圆的右焦点F2作一条直线l交椭圆与P、Q两点,则△F1PQ内切圆面积的最大值是
的左、右焦点分别为F1、F2,过椭圆的右焦点F2作一条直线l交椭圆与P、Q两点,则△F1PQ内切圆面积的最大值是 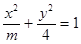 ,对于任意实数
,对于任意实数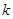 下列直线被椭圆E截得的弦长与直线
下列直线被椭圆E截得的弦长与直线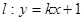 被椭圆E截得的弦长不可能相等的是( )
被椭圆E截得的弦长不可能相等的是( )

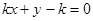

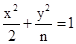 的离心率为
的离心率为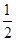 ,则n=( )
,则n=( )


