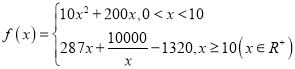题目内容
【题目】如图,在三棱柱![]() 中,
中,![]() 是边长为2的等边三角形,
是边长为2的等边三角形,![]() ,
,![]() ,
,![]() .
.
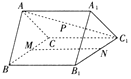
(1)证明:平面![]() 平面
平面![]() ;
;
(2)![]() ,
,![]() 分别是
分别是![]() ,
,![]() 的中点,
的中点,![]() 是线段
是线段![]() 上的动点,若二面角
上的动点,若二面角![]() 的平面角的大小为
的平面角的大小为![]() ,试确定点
,试确定点![]() 的位置.
的位置.
【答案】(1)证明见解析;(2)![]() 为线段
为线段![]() 上靠近
上靠近![]() 点的四等分点,且坐标为
点的四等分点,且坐标为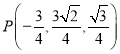
【解析】
(1)先通过线面垂直的判定定理证明![]() 平面
平面![]() ,再根据面面垂直的判定定理即可证明;
,再根据面面垂直的判定定理即可证明;
(2)分析位置关系并建立空间直角坐标系,根据二面角![]() 的余弦值与平面法向量夹角的余弦值之间的关系,即可计算出
的余弦值与平面法向量夹角的余弦值之间的关系,即可计算出![]() 的坐标从而位置可确定.
的坐标从而位置可确定.
(1)证明:因为![]() ,
,![]() ,
,![]() ,
,
所以![]() ,即
,即![]() .
.
又因为![]() ,
,![]() ,所以
,所以![]() ,
,
![]() ,所以
,所以![]() 平面
平面![]() .
.
因为![]() 平面
平面![]() ,所以平面
,所以平面![]() 平面
平面![]() .
.
(2)解:连接![]() ,因为
,因为![]() ,
,![]() 是
是![]() 的中点,所以
的中点,所以![]() .
.
由(1)知,平面![]() 平面
平面![]() ,所以
,所以![]() 平面
平面![]() .
.
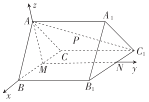
以![]() 为原点建立如图所示的空间直角坐标系
为原点建立如图所示的空间直角坐标系![]() ,
,
则平面![]() 的一个法向量是
的一个法向量是![]() ,
,![]() ,
,![]() ,
,![]() .
.
设![]() ,
,![]() ,
,
![]() ,
,![]() ,
,
代入上式得![]() ,
,![]() ,
,![]() ,所以
,所以![]() .
.
设平面![]() 的一个法向量为
的一个法向量为![]() ,
,![]() ,
,![]() ,
,
由 ,得
,得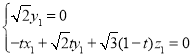 .
.
令![]() ,得
,得![]() .
.
因为二面角![]() 的平面角的大小为
的平面角的大小为![]() ,
,
所以![]() ,即
,即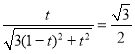 ,解得
,解得![]() .
.
所以点![]() 为线段
为线段![]() 上靠近
上靠近![]() 点的四等分点,且坐标为
点的四等分点,且坐标为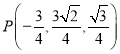 .
.

 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案【题目】为调研高中生的作文水平.在某市普通高中的某次联考中,参考的文科生与理科生人数之比为![]() ,且成绩分布在
,且成绩分布在![]() 的范围内,规定分数在50以上(含50)的作文被评为“优秀作文”,按文理科用分层抽样的方法抽取400人的成绩作为样本,得到成绩的频率分布直方图,如图所示.其中
的范围内,规定分数在50以上(含50)的作文被评为“优秀作文”,按文理科用分层抽样的方法抽取400人的成绩作为样本,得到成绩的频率分布直方图,如图所示.其中![]() 构成以2为公比的等比数列.
构成以2为公比的等比数列.
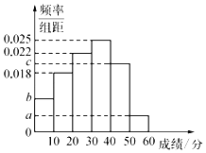
(1)求![]() 的值;
的值;
(2)填写下面![]() 列联表,能否在犯错误的概率不超过0.01的情况下认为“获得优秀作文”与“学生的文理科”有关?
列联表,能否在犯错误的概率不超过0.01的情况下认为“获得优秀作文”与“学生的文理科”有关?
文科生 | 理科生 | 合计 | |
获奖 | 6 | ||
不获奖 | |||
合计 | 400 |
(3)将上述调查所得的频率视为概率,现从全市参考学生中,任意抽取2名学生,记“获得优秀作文”的学生人数为![]() ,求
,求![]() 的分布列及数学期望.
的分布列及数学期望.
附: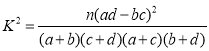 ,其中
,其中![]() .
.
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
【题目】某啤酒厂要将一批鲜啤酒用汽车从所在城市甲运至城市乙,已知从城市甲到城市乙只有两条公路,运费由厂家承担.若厂家恰能在约定日期(×月×日)将啤酒送到,则城市乙的销售商一次性支付给厂家40万元;若在约定日期前送到,每提前一天销售商将多支付给厂家2万;若在约定日期后送到,每迟到一天销售商将少支付给厂家2万元.为保证啤酒新鲜度,汽车只能在约定日期的前两天出发,且只能选择其中的一条公路运送.已知下表内的信息:
汽车行驶路线 | 在不堵车的情况下到达城市乙所需时间(天) | 在堵车的情况下到达城市乙所需时间(天) | 堵车的概率 | 运费(万元) |
公路1 | 1 | 4 |
| 2 |
公路2 | 2 | 3 |
| 1 |
(1)记汽车选择公路1运送啤酒时厂家获得的毛收入为X(单位:万元),求X的分布列和EX;
(2)若![]() ,
,![]() ,选择哪条公路运送啤酒厂家获得的毛收人更多?
,选择哪条公路运送啤酒厂家获得的毛收人更多?
(注:毛收入=销售商支付给厂家的费用-运费).