Question

12．已知函数f（x）=|2x-1|+|2x-a|，g（x）=x+3．
（1）当a=2时，求f（x）＜g（x）的解集；
（2）设a＞-1，当x∈[-$\frac{a}{2}$，$\frac{1}{2}$），f（x）≤g（x），求a的取值范围．

Answer 1

分析 （1）当a=-2时，求不等式f（x）＜g（x）化为|2x-1|+|2x-2|-x-3＜0．设y=|2x-1|+|2x-2|-x-3，画出函数y的图象，数形结合可得结论．
（2）不等式化即 1+a≤x+3，故 x≥a-2对x∈[-$\frac{a}{2}$，$\frac{1}{2}$）都成立．故-$\frac{a}{2}$≥a-2，由此解得a的取值范围．

解答 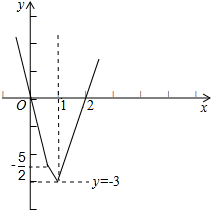解：（1）当a=-2时，求不等式f（x）＜g（x）化为|2x-1|+|2x-2|-x-3＜0．
设y=|2x-1|+|2x-2|-x-3，则y=$\left\{\begin{array}{l}{-5x，x＜\frac{1}{2}}\\{-x-2，\frac{1}{2}≤x≤1}\\{3x-6，x＞1}\end{array}\right.$，
它的图象如图所示：
结合图象可得，y＜0的解集为（0，2），故原不等式的解集为（0，2）．
（2）设a＞-1，且当x∈[-$\frac{a}{2}$，$\frac{1}{2}$）时，f（x）=1+a，
不等式化为 1+a≤x+3，故 x≥a-2对x∈[-$\frac{a}{2}$，$\frac{1}{2}$）都成立．
故-$\frac{a}{2}$≥a-2，解得a≤$\frac{4}{3}$，故a的取值范围为（-1，$\frac{4}{3}$]．

点评 本题主要考查绝对值不等式的解法，函数的恒成立问题，函数的单调性的应用，体现了数形结合以及转化的数学思想，属于中档题．