题目内容
在△ABC中，角A、B、C的对边分别是a、b、c，若（acosC+ccosA）sinB=
b，则角B的值为（ ）
| ||
| 2 |
A．
| B．
| C．
| D．
|
已知等式利用正弦定理化简得：（sinAcosC+sinCcosA）sinB=sin（A+C）sinB=
sinB，
∵sinB≠0，∴sin（A+C）=sinB=
，
∵B为三角形的内角，
∴B=
或
．
故选D
| ||
| 2 |
∵sinB≠0，∴sin（A+C）=sinB=
| ||
| 2 |
∵B为三角形的内角，
∴B=
| π |
| 3 |
| 2π |
| 3 |
故选D
练习册系列答案
相关题目
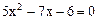的根，则三角形的另一边长为 .
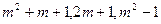，则此三角形最大角为 
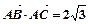，∠BAC=30°，设M是△ABC内的一点(不在边界上)，定义f(M)=(x,y,z)，其中x,y,z分别表示△MBC，△MC
A,△MAB的面积，若f(M)=(x,y,
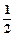)，则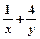
的最小值为( )