题目内容
△ABC中A,B,C的对边分别为a,b,c,且sin(B+C)+2sinA•cosB=0
求:(1)角B的大小;
(2)若b=
,a+c=4,求△ABC的面积.
求:(1)角B的大小;
(2)若b=
| 13 |
(1)∵B+C=π-A,∴sin(B+C)=sinA
由此可得sinA+2sinA•cosB=0,即sinA(1+2cosB)=0
∵sinA>0,∴1+2cosB=0,可得cosB=-
∵B∈(0,π),∴B=
.
(2)∵b=
,a+c=4,
∴根据余弦定理,得b2=a2+c2-2accos120°,
可得13=(a+c)2-ac=16-ac,解得ac=3
因此,△ABC的面积S=
acsinB=
×3×sin120°=
.
由此可得sinA+2sinA•cosB=0,即sinA(1+2cosB)=0
∵sinA>0,∴1+2cosB=0,可得cosB=-
| 1 |
| 2 |
∵B∈(0,π),∴B=
| 2π |
| 3 |
(2)∵b=
| 13 |
∴根据余弦定理,得b2=a2+c2-2accos120°,
可得13=(a+c)2-ac=16-ac,解得ac=3
因此,△ABC的面积S=
| 1 |
| 2 |
| 1 |
| 2 |
3
| ||
| 4 |

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
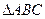 中,已知AB=5,BC=8,
中,已知AB=5,BC=8,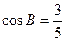
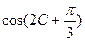 的值。
的值。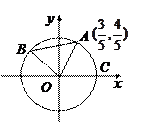
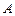 、
、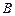 是单位圆
是单位圆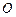 上的动点,
上的动点, 是圆与
是圆与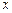 轴正半轴的交点,设
轴正半轴的交点,设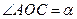 .
.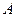 的坐标为
的坐标为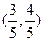 时,求
时,求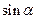 的值;
的值;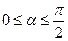 ,且当点A、B在圆上沿逆时针方向移动时总有
,且当点A、B在圆上沿逆时针方向移动时总有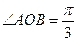 ,试求
,试求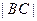 的取值范围.
的取值范围.