题目内容
三角形ABC中,a,b,c分别为角A,B,C所对的边,a=5,b=6,c=7,则abcosC+bccosA+cacosB=______.
∵由余弦定理,得a2=b2+c2-2bccosA,b2=a2+c2-2accosB,c2=a2+b2-2abcosC,
∴将三个式子相加,可得a2+b2+c2=2(a2+b2+c2)-2(abcosC+bccosA+cacosB),
整理得:abcosC+bccosA+cacosB=
(a2+b2+c2),
∵a=5,b=6,c=7,
∴abcosC+bccosA+cacosB=
(52+62+72)=55.
故答案为:55
∴将三个式子相加,可得a2+b2+c2=2(a2+b2+c2)-2(abcosC+bccosA+cacosB),
整理得:abcosC+bccosA+cacosB=
| 1 |
| 2 |
∵a=5,b=6,c=7,
∴abcosC+bccosA+cacosB=
| 1 |
| 2 |
故答案为:55

练习册系列答案
 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案
相关题目


 表示b;
表示b;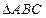 中,
中,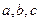 分别为角
分别为角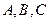 所对的边,且
所对的边,且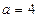 ,
,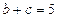 ,
,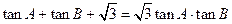 ,试求
,试求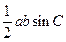 =
=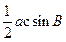 =
=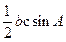 ).
).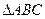 中,
中, ,
, ,
, ,则边
,则边 .
. ,则
,则 ( )
( )


