题目内容
【题目】设命题![]() :函数
:函数![]() 的定义域为
的定义域为![]() ;命题
;命题![]() :不等式
:不等式![]() 对一切正实数
对一切正实数![]() 均成立.
均成立.
(1)如果![]() 是真命题,求实数
是真命题,求实数![]() 的取值范围;
的取值范围;
(2)如果命题“![]() ”为真命题,且“
”为真命题,且“![]() ”为假命题,求实数
”为假命题,求实数![]() 的取值范围.
的取值范围.
【答案】(1)![]() (2)
(2)![]()
【解析】
(1)利用命题![]() 是真命题,函数恒成立,列出不等式组求解a的范围即可.
是真命题,函数恒成立,列出不等式组求解a的范围即可.
(2)求出q是真命题时,a的范围,利用复合命题的真假可得命题![]() 与命题
与命题![]() 一真一假,列不等式求解a的范围即可.
一真一假,列不等式求解a的范围即可.
(1)由题意知,![]() 对一切实数
对一切实数![]() 恒成立,
恒成立,
若![]() ,不合题意,舍去;
,不合题意,舍去;
若![]() ,由
,由![]() ,解得
,解得![]() ;
;
综上,实数![]() 的取值范围是
的取值范围是![]() .
.
(2)设![]() ,因为
,因为![]() ,所以
,所以![]() ,则
,则![]() ,
,
所以使得命题![]() 为真的实数
为真的实数![]() 的取值范围是
的取值范围是![]() ;
;
因为命题“![]() ”为真命题,且“
”为真命题,且“![]() ”为假命题,所以命题
”为假命题,所以命题![]() 与命题
与命题![]() 一真一假,
一真一假,
因此![]() ,此时无解,或
,此时无解,或![]() ,可得
,可得![]() ,
,
所以,所求实数![]() 的取值范围是
的取值范围是![]() .
.

【题目】某企业生产一种产品,从流水线上随机抽取![]() 件产品,统计其质量指标值并绘制频率分布直方图(如图1):规定产品的质量指标值在
件产品,统计其质量指标值并绘制频率分布直方图(如图1):规定产品的质量指标值在![]() 的为劣质品,在
的为劣质品,在![]() 的为优等品,在
的为优等品,在![]() 的为特优品,销售时劣质品每件亏损
的为特优品,销售时劣质品每件亏损![]() 元,优等品每件盈利
元,优等品每件盈利![]() 元,特优品每件盈利
元,特优品每件盈利![]() 元,以这
元,以这![]() 件产品的质量指标值位于各区间的频率代替产品的质量指标值位于该区间的概率.
件产品的质量指标值位于各区间的频率代替产品的质量指标值位于该区间的概率.
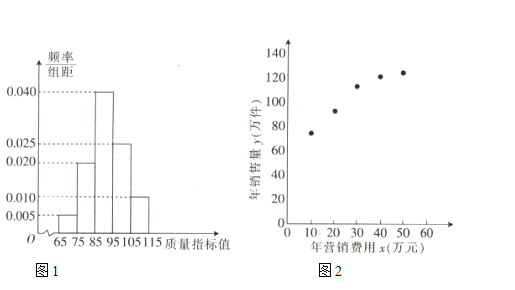
(1)求每件产品的平均销售利润;
(2)该企业主管部门为了解企业年营销费用![]() (单位:万元)对年销售量
(单位:万元)对年销售量![]() (单位:万件)的影响,对该企业近
(单位:万件)的影响,对该企业近![]() 年的年营销费用
年的年营销费用![]() 和年销售量
和年销售量![]() ,
,![]() 数据做了初步处理,得到的散点图(如图2)及一些统计量的值.
数据做了初步处理,得到的散点图(如图2)及一些统计量的值.
|
|
|
|
|
|
|
|
表中![]() ,
,![]() ,
,![]() ,
,![]() .
.
根据散点图判断,![]() 可以作为年销售量
可以作为年销售量![]() (万件)关于年营销费用
(万件)关于年营销费用![]() (万元)的回归方程.
(万元)的回归方程.
①求![]() 关于
关于![]() 的回归方程;
的回归方程;
②用所求的回归方程估计该企业每年应投入多少营销费,才能使得该企业的年收益的预报值达到最大?(收益![]() 销售利润
销售利润![]() 营销费用,取
营销费用,取![]() )
)
附:对于一组数据![]() ,
,![]() ,
,![]() ,
,![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘估计分别为
的斜率和截距的最小二乘估计分别为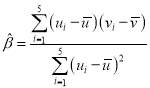 ,
,![]() .
.
【题目】某科研课题组通过一款手机APP软件,调查了某市1000名跑步爱好者平均每周的跑步量(简称“周跑量”),得到如下的频数分布表
周跑量(km/周) |
|
|
|
|
|
|
|
|
|
人数 | 100 | 120 | 130 | 180 | 220 | 150 | 60 | 30 | 10 |
(1)在答题卡上补全该市1000名跑步爱好者周跑量的频率分布直方图:

注:请先用铅笔画,确定后再用黑色水笔描黑
(2)根据以上图表数据计算得样本的平均数为![]() ,试求样本的中位数(保留一位小数),并用平均数、中位数等数字特征估计该市跑步爱好者周跑量的分布特点
,试求样本的中位数(保留一位小数),并用平均数、中位数等数字特征估计该市跑步爱好者周跑量的分布特点
(3)根据跑步爱好者的周跑量,将跑步爱好者分成以下三类,不同类别的跑者购买的装备的价格不一样,如下表:
周跑量 | 小于20公里 | 20公里到40公里 | 不小于40公里 |
类别 | 休闲跑者 | 核心跑者 | 精英跑者 |
装备价格(单位:元) | 2500 | 4000 | 4500 |
根据以上数据,估计该市每位跑步爱好者购买装备,平均需要花费多少元?
【题目】某地自2014年至2019年每年年初统计所得的人口数量如表所示:
年份 | 2014 | 2015 | 2016 | 2017 | 2018 | 2019 |
人数(单位:千人) | 2082 | 2135 | 2203 | 2276 | 2339 | 2385 |
(1)根据表中的数据判断从2014年到2019年哪个跨年度的人口增长数量最大?并描述该地人口数量的变化趋势;
(2)研究人员用函数![]() 拟合该地的人口数量,其中
拟合该地的人口数量,其中![]() 的单位是年,2014年年初对应时刻
的单位是年,2014年年初对应时刻![]() ,
,![]() 的单位是千人,经计算可得
的单位是千人,经计算可得![]() ,请解释
,请解释![]() 的实际意义.
的实际意义.