题目内容
已知函数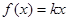 ,
,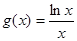
(1)求函数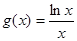 的单调递增区间;
的单调递增区间;
(2)若不等式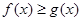 在区间(0,+
在区间(0,+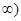 上恒成立,求
上恒成立,求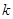 的取值范围;
的取值范围;
(3)求证:
(1) 函数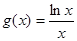 的单调递增区间为
的单调递增区间为
(2) 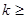
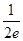 (3)在第二问的基础上,由(2)知
(3)在第二问的基础上,由(2)知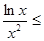
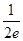 ,则可以放大得到∴
,则可以放大得到∴ 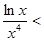
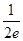
 (
(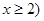 ,从而得证。
,从而得证。
解析试题分析:解:(1)∵ 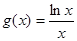 (
(
∴  令
令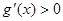 ,得
,得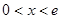
故函数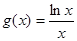 的单调递增区间为
的单调递增区间为 3分
3分
(2)由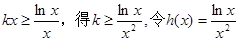
则问题转化为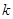 大于等于
大于等于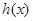 的最大值 5分
的最大值 5分
又 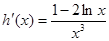 6分
6分
令 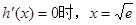
当 在区间(0,+
在区间(0,+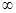 )内变化时,
)内变化时,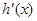 、
、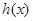 变化情况如下表:
变化情况如下表:
由表知当
(0, 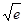 )
)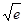
( 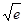 ,+
,+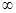 )
)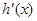
+ 0 — 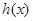
↗ 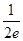
↘ 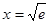 时,函数
时,函数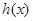 有最大值,且最大值为
有最大值,且最大值为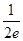 8分
8分
因此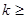
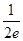 9分
9分
(3)由(2)知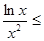
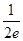 ,
,
∴ 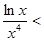
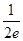
 (
(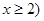 10分
10分
∴ (
(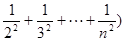 12分
12分
又∵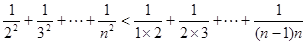
=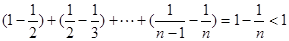
∴ 14分
14分
考点:导数的运用
点评:解决的关键是利用导数的符号确定单调性,以及函数与不等式的综合,属于基础题。

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
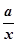 .
.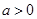 时,判断f(x)在定义域上的单调性;
时,判断f(x)在定义域上的单调性; ,求
,求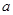 的值.
的值.
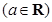 .
.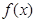 在定义域内的极值点的个数;
在定义域内的极值点的个数;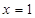 处取得极值,对
处取得极值,对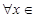
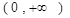 ,
, 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围. 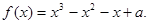
 的极值.
的极值.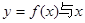 轴仅有一个交点.
轴仅有一个交点.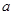 为实数,函数
为实数,函数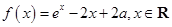 。
。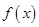 的单调区间与极值;
的单调区间与极值;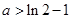 且
且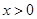 时,
时,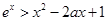 。
。 在区间[-1,1]上是增函数.
在区间[-1,1]上是增函数. 的两个非零实根为x1、x2.试问:是否存在实数m,使得不等式m2+tm+1≥|x1-x2|对任意a∈A及t∈[-1,1]恒成立?若存在,求m的取值范围;若不存在,请说明理由.
的两个非零实根为x1、x2.试问:是否存在实数m,使得不等式m2+tm+1≥|x1-x2|对任意a∈A及t∈[-1,1]恒成立?若存在,求m的取值范围;若不存在,请说明理由. (2)
(2)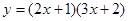
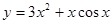 (4)
(4)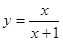

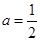 ,求
,求 的单调区间;
的单调区间; ≥0时
≥0时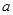 的取值范围.
的取值范围.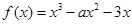
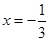 是
是 的极值点,求
的极值点,求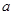 ]上的最大值;
]上的最大值; )上是增函数,求实数
)上是增函数,求实数