题目内容
已知函数
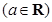 .
.
(1)讨论函数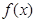 在定义域内的极值点的个数;
在定义域内的极值点的个数;
(2)若函数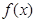 在
在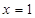 处取得极值,对
处取得极值,对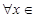
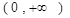 ,
, 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.
(Ⅰ)当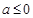 时
时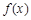 在
在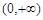 上没有极值点,当
上没有极值点,当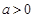 时,
时,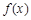 在
在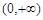 上有一个极值点.(Ⅱ)
上有一个极值点.(Ⅱ)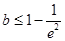 .
.
解析试题分析:(Ⅰ) ,
,
当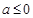 时,
时, 在
在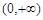 上恒成立,函数
上恒成立,函数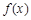 在
在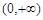 单调递减,
单调递减,
∴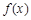 在
在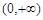 上没有极值点;
上没有极值点;
当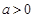 时,
时, 得
得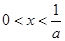 ,
,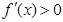 得
得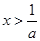 ,
,
∴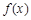 在
在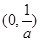 上递减,在
上递减,在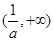 上递增,即
上递增,即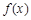 在
在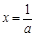 处有极小值.
处有极小值.
∴当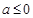 时
时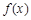 在
在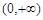 上没有极值点,
上没有极值点,
当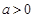 时,
时,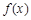 在
在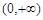 上有一个极值点.
上有一个极值点.
(Ⅱ)∵函数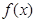 在
在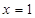 处取得极值,∴
处取得极值,∴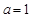 ,∴
,∴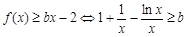 ,
,
令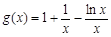 ,可得
,可得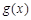 在
在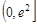 上递减,在
上递减,在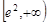 上递增,
上递增,
∴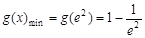 ,即
,即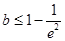 .
.
考点:本题考查了导数的运用
点评:求可导函数的极值的基本步骤为:①求导函数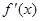 ;②求方程
;②求方程 =0的根;③检查
=0的根;③检查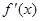 在方程根左右的符号,如果左正右负,那么f(x)在这个根处取得极大值;如果左负右正,那么f(x)在这个根处取得极小值.
在方程根左右的符号,如果左正右负,那么f(x)在这个根处取得极大值;如果左负右正,那么f(x)在这个根处取得极小值.

练习册系列答案
 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案
相关题目
 ,其中
,其中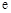 为自然对数的底数.
为自然对数的底数.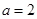 时,求曲线
时,求曲线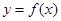 在
在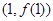 处的切线与坐标轴围成的三角形的面积;
处的切线与坐标轴围成的三角形的面积;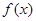 存在一个极大值和一个极小值,且极大值与极小值的积为
存在一个极大值和一个极小值,且极大值与极小值的积为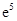 ,求
,求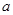 的
的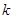 和
和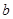 ,使得函数
,使得函数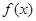 和
和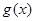 对其定义域上的任意实数
对其定义域上的任意实数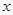 分别满足:
分别满足: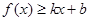 和
和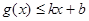 ,则称直线
,则称直线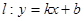 为
为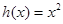 ,
,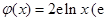 为自然对数的底数).
为自然对数的底数).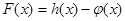 的极值;
的极值; 和
和 是否存在隔离直线?若存在,求出此隔离直线方程;若不存在,请说明理由.
是否存在隔离直线?若存在,求出此隔离直线方程;若不存在,请说明理由.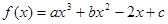 在
在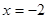 时有极大值6,在
时有极大值6,在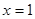 时有极小值
时有极小值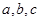 的值;并求
的值;并求 在区间[-3,3]上的最大值和最小值.
在区间[-3,3]上的最大值和最小值.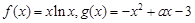 .
.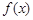 在
在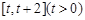 上的最小值;
上的最小值;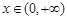 ,
,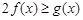 恒成立,求实数a的取值范围.
恒成立,求实数a的取值范围. .
.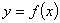 与曲线
与曲线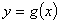 在它们的交点
在它们的交点 处具有公共切线,求
处具有公共切线,求 的值;
的值;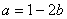 时,若函数
时,若函数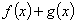 在区间
在区间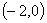 内恰有两个零点,求
内恰有两个零点,求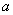 的取值范围;
的取值范围;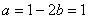 时,求函数
时,求函数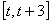 上的最大值
上的最大值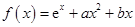 .
.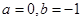 时,求
时,求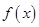 的单调区间;
的单调区间;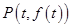
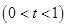 处的切线为
处的切线为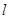 ,直线
,直线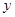 轴相交于点
轴相交于点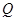 .若点
.若点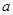 的取值范围.
的取值范围.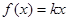 ,
,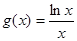
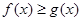 在区间(0,+
在区间(0,+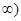 上恒成立,求
上恒成立,求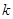 的取值范围;
的取值范围;
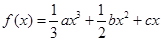 .(
.(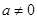 )
) 有三个零点
有三个零点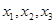 ,且
,且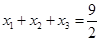 ,
,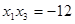 ,求函数
,求函数  的单调区间;
的单调区间; 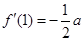 ,
,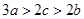 ,试问:导函数
,试问:导函数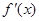 在区间(0,2)内是否有零点,并说明理由.
在区间(0,2)内是否有零点,并说明理由.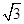 ,求
,求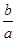 的取值范围.
的取值范围.