题目内容
(本小题满分12分)
设函数
(Ⅰ)若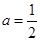 ,求
,求 的单调区间;
的单调区间;
(Ⅱ)若当 ≥0时
≥0时 ≥0,求
≥0,求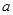 的取值范围.
的取值范围.
(I)函数的增区间为(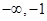 ),(
),(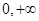 ),减区间为(-1,0).(II)a≤1。
),减区间为(-1,0).(II)a≤1。
解析试题分析:(I)若a等于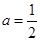 ,则
,则 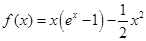 ,
,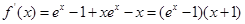
令f'(x)= 0得驻点x="0" ,x=-1
X<-1, f'(x)>0,f(x)单调递增;
-1<x<0, f'(x)<0,f(x)单调递减;
x>0,f'(x)>0,f(x)单调递增,故函数的增区间为(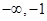 ),(
),(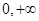 ),减区间为(-1,0).
),减区间为(-1,0).
(II)
若当 ≥0时
≥0时 ≥0,
≥0,
所以,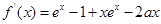
则当x=0时,有:f'(x)=0。且f(0)=0
已知当x≥0时,f(x)≥0
所以,必须满足在x>0时,f'(x)>0,
则:x>0时,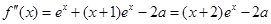
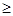 0,
0,
所以,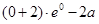 ≥0,得a≤1。
≥0,得a≤1。
考点:本题主要考查应用导数研究函数的单调性及极值,根据不等式成立求参数值。
点评:典型题,本题属于导数应用中的基本问题,(II)通过研究函数的单调性,函数值与最值比较,达到解题目的。

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
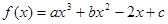 在
在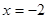 时有极大值6,在
时有极大值6,在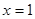 时有极小值
时有极小值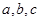 的值;并求
的值;并求 在区间[-3,3]上的最大值和最小值.
在区间[-3,3]上的最大值和最小值.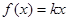 ,
,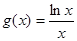
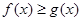 在区间(0,+
在区间(0,+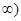 上恒成立,求
上恒成立,求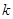 的取值范围;
的取值范围;
 在区间
在区间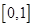 上是增函数,在区间
上是增函数,在区间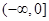 和
和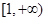 上是减函数,且
上是减函数,且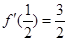
 的解析式.
的解析式.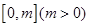 上恒有
上恒有 ,求实数
,求实数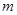 的取值范围.
的取值范围.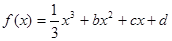 ,设曲线
,设曲线 在与
在与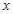 轴交点处的切线为
轴交点处的切线为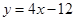 ,
,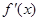 为
为 的导函数,满足
的导函数,满足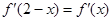 .
.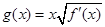 ,
,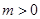 ,求函数
,求函数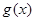 在
在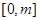 上的最大值;
上的最大值; 在
在 处取得极值,且在
处取得极值,且在 处的切线的斜率为1。
处的切线的斜率为1。 的值及
的值及 的单调减区间;
的单调减区间; >0,
>0, >0,
>0, ,求证:
,求证: 。
。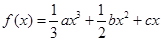 .(
.(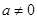 )
) 有三个零点
有三个零点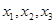 ,且
,且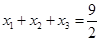 ,
,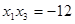 ,求函数
,求函数  的单调区间;
的单调区间; 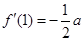 ,
,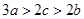 ,试问:导函数
,试问:导函数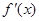 在区间(0,2)内是否有零点,并说明理由.
在区间(0,2)内是否有零点,并说明理由.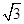 ,求
,求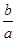 的取值范围.
的取值范围. .
. 在
在 ,
, 处取得极值,求
处取得极值,求 ,
, 的值;
的值; ,函数
,函数 上是单调函数,求
上是单调函数,求 ,其中
,其中 是自然对数的底数,
是自然对数的底数,
 时,
时, 的单调性。
的单调性。
 ,使
,使