题目内容
设a为实数, 函数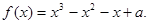
(Ⅰ)求 的极值.
的极值.
(Ⅱ)当a在什么范围内取值时,曲线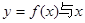 轴仅有一个交点.
轴仅有一个交点.
(Ⅰ) 极大值是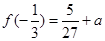 ,极小值是
,极小值是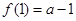 ;(Ⅱ)
;(Ⅱ) 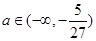 ∪(1,+∞)。
∪(1,+∞)。
解析试题分析:(I)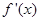 =3
=3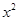 -2
-2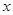 -1若
-1若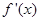 =0,则
=0,则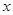 ==-
==- ,
,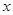 =1
=1
当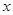 变化时,
变化时,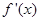 ,
, 变化情况如下表:
变化情况如下表:
∴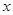
(-∞,-  )
)- 
(-  ,1)
,1)1 (1,+∞) 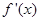
+ 0 - 0 + 

极大值 
极小值 
 的极大值是
的极大值是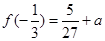 ,极小值是
,极小值是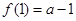 --------8分
--------8分
(II)由(I)可知,取足够大的正数时,有 >0,取足够小的负数时有
>0,取足够小的负数时有 <0,
<0,
结合 的单调性可知:
的单调性可知: <0,或
<0,或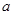 -1>0时,曲线
-1>0时,曲线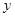 =
= 与
与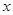 轴仅有一个交点,
轴仅有一个交点,
∴当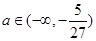 ∪(1,+∞)时,曲线
∪(1,+∞)时,曲线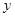 =
= 与
与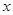 轴仅有一个交点。 14分
轴仅有一个交点。 14分
考点:利用导数研究函数的极值;利用导数研究函数的单调性。
点评:做此题的关键是分析出:要满足题意只需极大值小于0或者极小值大于0.考查了学生分析问题,解决问题的能力。属于中档题型。

练习册系列答案
 星级口算天天练系列答案
星级口算天天练系列答案
相关题目
 元(
元(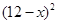 万件.
万件.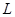 (万元)与每件产品的售价
(万元)与每件产品的售价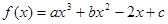 在
在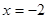 时有极大值6,在
时有极大值6,在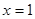 时有极小值
时有极小值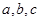 的值;并求
的值;并求 在区间[-3,3]上的最大值和最小值.
在区间[-3,3]上的最大值和最小值. .
.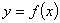 与曲线
与曲线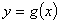 在它们的交点
在它们的交点 处具有公共切线,求
处具有公共切线,求 的值;
的值;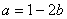 时,若函数
时,若函数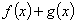 在区间
在区间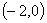 内恰有两个零点,求
内恰有两个零点,求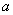 的取值范围;
的取值范围;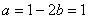 时,求函数
时,求函数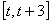 上的最大值
上的最大值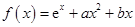 .
.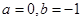 时,求
时,求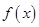 的单调区间;
的单调区间;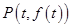
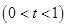 处的切线为
处的切线为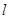 ,直线
,直线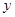 轴相交于点
轴相交于点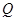 .若点
.若点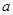 的取值范围.
的取值范围. ,
,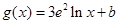 (
( ,
,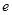 为常数,
为常数,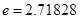 ),且这两函数的图像有公共点,并在该公共点处的切线相同.
),且这两函数的图像有公共点,并在该公共点处的切线相同. 的值;
的值;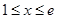 时,
时,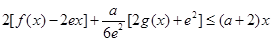 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.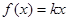 ,
,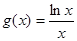
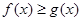 在区间(0,+
在区间(0,+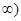 上恒成立,求
上恒成立,求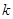 的取值范围;
的取值范围;
 在区间
在区间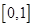 上是增函数,在区间
上是增函数,在区间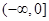 和
和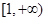 上是减函数,且
上是减函数,且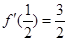
 的解析式.
的解析式.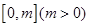 上恒有
上恒有 ,求实数
,求实数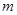 的取值范围.
的取值范围. .
. 在
在 ,
, 处取得极值,求
处取得极值,求 ,
, 的值;
的值; ,函数
,函数 上是单调函数,求
上是单调函数,求