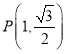题目内容
【题目】已知点![]() 到抛物线C:y2=2px
到抛物线C:y2=2px![]() 准线的距离为2.
准线的距离为2.
(Ⅰ)求C的方程及焦点F的坐标;
(Ⅱ)设点P关于原点O的对称点为点Q,过点Q作不经过点O的直线与C交于两点A,B,直线PA,PB,分别交x轴于M,N两点,求![]() 的值.
的值.
【答案】(Ⅰ)C的方程为![]() ,焦点F的坐标为(1,0);(Ⅱ)2
,焦点F的坐标为(1,0);(Ⅱ)2
【解析】
(Ⅰ)根据抛物线定义求出p,即可求C的方程及焦点F的坐标;
(Ⅱ)设点A(x1,y1),B(x2,y2),由已知得Q(1,2),由题意直线AB斜率存在且不为0,设直线AB的方程为y=k(x+1)2(k≠0),与抛物线联立可得ky2-4y+4k-8=0,利用韦达定理以及弦长公式,转化求解|MF||NF|的值.

(Ⅰ)由已知得![]() ,所以p=2.
,所以p=2.
所以抛物线C的方程为![]() ,焦点F的坐标为(1,0);
,焦点F的坐标为(1,0);
(II)设点A(x1,y1),B(x2,y2),由已知得Q(1,2),
由题意直线AB斜率存在且不为0.
设直线AB的方程为y=k(x+1)2(k≠0).
由 得
得![]() ,
,
则![]() ,
,![]() .
.
因为点A,B在抛物线C上,所以![]()
 ,
,![]() .
.
因为PF⊥x轴,
所以
 ,
,
所以|MF||NF|的值为2.

练习册系列答案
相关题目