题目内容
已知直线l:x+y-2=0,一束光线过点P(0,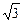 +1),以120°的倾斜角投射到l上,经过l反射,求反射光线所在直线的方程.
+1),以120°的倾斜角投射到l上,经过l反射,求反射光线所在直线的方程.
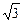 +1),以120°的倾斜角投射到l上,经过l反射,求反射光线所在直线的方程.
+1),以120°的倾斜角投射到l上,经过l反射,求反射光线所在直线的方程.反射光线所在直线的方程为y-1=-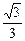 (x-1),即x+
(x-1),即x+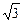 y-
y-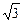 -1=0.
-1=0.
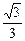 (x-1),即x+
(x-1),即x+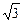 y-
y-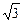 -1=0.
-1=0.欲求反射光线所在直线的方程,可考虑以下途径:
(1)求出倾斜角;
(2)求出斜率;
(3)求出它经过的两个特殊点;
(4)考虑对称关系.
解法一:建立坐标系如下图,设入射光线交l于Q点,交x轴于M点,反射光线交x轴于P2点,l交x轴于N点.
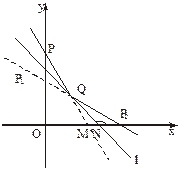
∵∠QMP2=120°,∠QNP2=135°,∴∠MQN=15°.
由光的反射定理知∠MQN=∠NQP2=15°,故反射光线的倾斜角θ=120°+30°=150°.
∴所求直线的斜率为-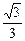 .
.
由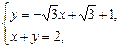 得Q(1,1).
得Q(1,1).
故反射光线所在直线的方程为y-1=-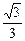 (x-1),
(x-1),
即x+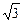 y-
y-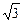 -1=0.
-1=0.
解法二:kλ=-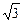 ,设反射光线的斜率为k,由入射光线到l的角等于l到反射光线的角,所以有
,设反射光线的斜率为k,由入射光线到l的角等于l到反射光线的角,所以有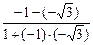 =
=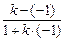 .
.
解之得k=-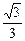 .
.
由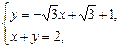 得Q(1,1).
得Q(1,1).
故反射光线所在直线的方程为y-1=-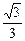 (x-1),即x+
(x-1),即x+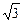 y-
y-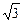 -1=0.
-1=0.
(1)求出倾斜角;
(2)求出斜率;
(3)求出它经过的两个特殊点;
(4)考虑对称关系.
解法一:建立坐标系如下图,设入射光线交l于Q点,交x轴于M点,反射光线交x轴于P2点,l交x轴于N点.

∵∠QMP2=120°,∠QNP2=135°,∴∠MQN=15°.
由光的反射定理知∠MQN=∠NQP2=15°,故反射光线的倾斜角θ=120°+30°=150°.
∴所求直线的斜率为-
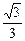 .
.由
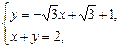 得Q(1,1).
得Q(1,1).故反射光线所在直线的方程为y-1=-
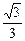 (x-1),
(x-1),即x+
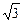 y-
y-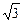 -1=0.
-1=0.解法二:kλ=-
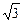 ,设反射光线的斜率为k,由入射光线到l的角等于l到反射光线的角,所以有
,设反射光线的斜率为k,由入射光线到l的角等于l到反射光线的角,所以有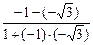 =
=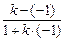 .
.解之得k=-
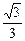 .
.由
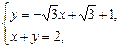 得Q(1,1).
得Q(1,1).故反射光线所在直线的方程为y-1=-
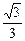 (x-1),即x+
(x-1),即x+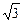 y-
y-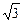 -1=0.
-1=0.
练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
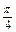 ,求直线l的方程.
,求直线l的方程.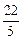 )、P(x,y)在△ABC表示的区域内(包括边界)且目标函数z=ax+y(a>0)取得最大值的最优解有无穷多个,则a的值为
)、P(x,y)在△ABC表示的区域内(包括边界)且目标函数z=ax+y(a>0)取得最大值的最优解有无穷多个,则a的值为
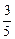
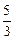
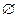
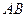 在直线
在直线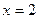 上移动,
上移动, 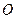 为原点.
为原点. 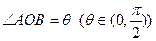 , 动点
, 动点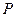 满足
满足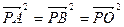 .
.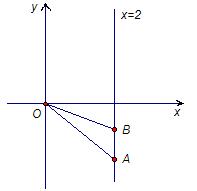
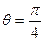 时, 动点
时, 动点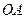 交于
交于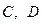 两点(点
两点(点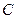 在点
在点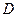 的下方), 且
的下方), 且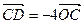 , 求直线
, 求直线