题目内容
已知直线l经过两条直线l1:x+2y=0与l2:3x-4y-10=0的交点,且与直线l3:5x-2y+3=0的夹角为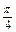 ,求直线l的方程.
,求直线l的方程.
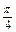 ,求直线l的方程.
,求直线l的方程.7x+3y-11=0或3x-7y-13=0
由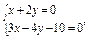
解得l1和l2的交点坐标为(2,-1).
设所求直线l的方程为y+1=k(x-2).
又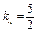 ,由l与l3的夹角为
,由l与l3的夹角为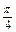
得tan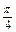 =
=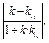 ,
,
即1=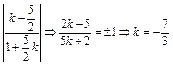 或k=
或k=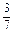 .
.
故所求的直线l的方程为
y+1=-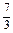 (x-2)或y+1=
(x-2)或y+1=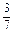 (x-2),
(x-2),
即7x+3y-11=0或3x-7y-13=0.
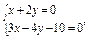
解得l1和l2的交点坐标为(2,-1).
设所求直线l的方程为y+1=k(x-2).
又
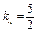 ,由l与l3的夹角为
,由l与l3的夹角为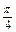
得tan
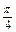 =
=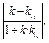 ,
,即1=
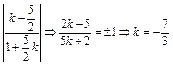 或k=
或k=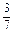 .
.故所求的直线l的方程为
y+1=-
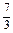 (x-2)或y+1=
(x-2)或y+1=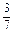 (x-2),
(x-2),即7x+3y-11=0或3x-7y-13=0.

练习册系列答案
相关题目
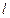 过点
过点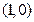 ,且与直线
,且与直线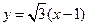 的夹角为
的夹角为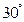 ,求直线
,求直线 ,求直线l的方程.
,求直线l的方程. 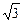 +1),以120°的倾斜角投射到l上,经过l反射,求反射光线所在直线的方程.
+1),以120°的倾斜角投射到l上,经过l反射,求反射光线所在直线的方程.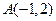 ,
,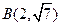 ,在
,在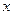 轴上求一点
轴上求一点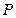 ,使
,使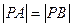 ,并求
,并求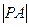 的值.
的值.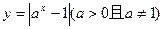 图象有两个交点,则a的取值范围是
图象有两个交点,则a的取值范围是