题目内容
10.已知函数f(x)=ax2+x-2,g(x)=-x+1+4lnx,h(x)=f(x)-g(x).(1)当a=1时,证明函数h(x)只有一个零点;
(2)若a<0,已知函数h(x)在定义域内没有极值点,求实数a的范围.
分析 (1)求导函数,确定函数的单调性,即可得出函数的零点.
(2)通过f(x)在定义域内无极值,f′(x)≤0在定义域上恒成立,分离参数,构造函数,求出函数的最小值即可求实数a的取值范围.
解答 解:(1)∵当a=1时,f(x)=x2+x-2,g(x)=-x+1+4lnx,
∴h(x)=f(x)-g(x)=x2+x-2+x-1-4lnx=x2+2x-3-4lnx,x>0,
∴h′(x)=2x+2-$\frac{4}{x}$=$\frac{2({x}^{2}+x-2)}{x}$=$\frac{2(x+2)(x-1)}{x}$,
令h′(x)=0,解得x=1,
当0<x<1时,h′(x)<0;当x>1时,f′(x)>0.
∴函数h(x)在区间(0,1)上单调递减,在区间(1,+∞)上单调递增,
∴当x=1时,函数f(x)取得最小值,其值为h(1)=1+2-3-4ln1=0.
当x≠1时,h(x)>f(1),即h(x)>0.
∴函数h(x)只有一个零点,
(2)h(x)=ax2+2x-3-4lnx,(x>0),
∴h′(x)=2ax+2-$\frac{4}{x}$=$\frac{2(a{x}^{2}+x-2)}{x}$,(a<0)
∵h(x)在定义域内无极值,
∴h′(x)≤0在定义域上恒成立,
∴ax2+x-2≤0恒成立,
∴a≤$\frac{2}{{x}^{2}}$-$\frac{1}{x}$,在(0,+∞)恒成立,
设F(x)=$\frac{2}{{x}^{2}}$-$\frac{1}{x}$,
∴F′(x)=-$\frac{4}{{x}^{3}}$+$\frac{1}{{x}^{2}}$=$\frac{x-4}{{x}^{3}}$,
令F′(x)=0,解得x=4,
当0<x<4时,F′(x)<0;当x>4时,F′(x)>0.
∴函数F(x)在区间(0,4)上单调递减,在区间(4,+∞)上单调递增,
∴当x=4时,函数F(x)取得最小值,其值为F(4)=$\frac{1}{8}$-$\frac{1}{4}$=-$\frac{1}{8}$,
∴a<-$\frac{1}{8}$.
点评 本题考查函数的零点,考查导数和函数的单调性极值最值得关系,以及函数恒成立等问题,考查学生分析解决问题的能力,属于中档题.

 同步练习强化拓展系列答案
同步练习强化拓展系列答案| A. | 4$\sqrt{3}$ | B. | 4+4$\sqrt{3}$ | C. | 4+4$\sqrt{2}$ | D. | 4+8$\sqrt{3}$ |
| A. | S正<S球<S柱 | B. | S正<S柱<S球 | C. | S球<S柱<S正 | D. | S球<S正<S柱 |
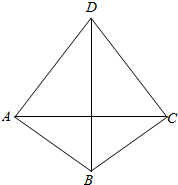 如图,在四边形ABCD中,AC=$\sqrt{3}$,∠ABC=120°,∠BAD=∠BCD=90°,则BD的长为4.
如图,在四边形ABCD中,AC=$\sqrt{3}$,∠ABC=120°,∠BAD=∠BCD=90°,则BD的长为4.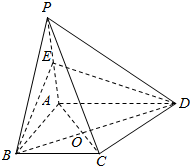 在四棱锥P-ABCD中,底面ABCD是梯形,BC∥AD,AD=2BC,AC交BD于点O,试问在棱PA上是否存在点E,使得直线PC∥平面EBD?若存在,求PE:PA的值,并证明你的结论.若不存在,请说明理由.
在四棱锥P-ABCD中,底面ABCD是梯形,BC∥AD,AD=2BC,AC交BD于点O,试问在棱PA上是否存在点E,使得直线PC∥平面EBD?若存在,求PE:PA的值,并证明你的结论.若不存在,请说明理由.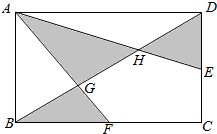 如图:长方体ABCD中,AB=10厘米,BC=15厘米,E,F分别是所在边的中点,求阴影部分的面积.(提示:由于图中AD平行于BC,可知AD:BF=AG:CF=DG:BG)
如图:长方体ABCD中,AB=10厘米,BC=15厘米,E,F分别是所在边的中点,求阴影部分的面积.(提示:由于图中AD平行于BC,可知AD:BF=AG:CF=DG:BG)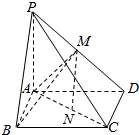 已知在四棱锥P-ABCD中,平面ABCD是平行四边形,侧棱PA⊥平面ABCD,M、N分别为PD、AC的中点.
已知在四棱锥P-ABCD中,平面ABCD是平行四边形,侧棱PA⊥平面ABCD,M、N分别为PD、AC的中点.