题目内容
5.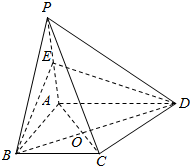 在四棱锥P-ABCD中,底面ABCD是梯形,BC∥AD,AD=2BC,AC交BD于点O,试问在棱PA上是否存在点E,使得直线PC∥平面EBD?若存在,求PE:PA的值,并证明你的结论.若不存在,请说明理由.
在四棱锥P-ABCD中,底面ABCD是梯形,BC∥AD,AD=2BC,AC交BD于点O,试问在棱PA上是否存在点E,使得直线PC∥平面EBD?若存在,求PE:PA的值,并证明你的结论.若不存在,请说明理由.
分析 取AD中点F,AF=FD,连接CF,BD,CF交BD于Q,由已知条播是到四边形ABCF是平行四边形,四边形BCDF平行四边形,由此能推导出存在PC∥平面EBD,且必有PC∥EO,并能求出PE:PA的值.
解答  解:存在PC∥平面EBD.
解:存在PC∥平面EBD.
证明如下:取AD中点F,AF=FD,连接CF,BD,CF交BD于Q,
由已知得AD=2BC=2AF=2FD,故AF=FD=BC,
∵BC∥AF,BC∥DF,
∴四边形ABCF是平行四边形,四边形BCDF平行四边形,
∴AB=2CQ,
又∵CQ∥AB,∴$\frac{AO}{CO}$=$\frac{AB}{QC}$,
∴$\frac{AO}{OC}=\frac{2}{1},\frac{CO}{CA}=\frac{1}{3}$,
∴存在PC∥平面EBD,且必有PC∥EO,
∴PE:PA=CO:CA=1:3.
点评 本题考查线面平行判断与证明,是中档题,解题时要认真审题,注意空间中线线、线面、面面间的位置关系的合理运用.

练习册系列答案
相关题目
6.根据下表,绘制网络图.
| 工作代码 | 紧前工作 | 紧后工作 | 工期/时 |
| A | C | G | 2 |
| B | D | 无 | 3 |
| C | 无 | A、D、F | 4 |
| D | C | B | 2 |
| E | F | 无 | 4 |
| F | C | E | 2 |
| G | A | 无 | 5 |
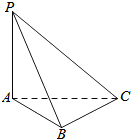 如图所示,PA⊥平面ABC,AC⊥BC,AB=2,BC=$\sqrt{2}$,PB=$\sqrt{6}$,则二面角P-BC-A的大小为45°.
如图所示,PA⊥平面ABC,AC⊥BC,AB=2,BC=$\sqrt{2}$,PB=$\sqrt{6}$,则二面角P-BC-A的大小为45°.