题目内容
【题目】为了竖一块广告牌，要制造三角形支架，如图，要求∠ACB=60°，BC的长度大于1米，且AC比AB长0.5米，为了稳固广告牌，要求AC越短越好，则AC最短为（ ） 
A.（1+ 
）米
B.2米
C.（1+ 
）米
D.（2+ ）米
【答案】D
【解析】解：设BC的长度为x米，AC的长度为y米，则AB的长度为（y﹣0.5）米， 在△ABC中，依余弦定理得：AB2=AC2+BC2﹣2ACBCcos∠ACB，
即（y﹣0.5）2=y2+x2﹣2yx× 
，化简，得y（x﹣1）=x2﹣ 
，
∵x＞1，
∴x﹣1＞0，
因此y= 
，
y=（x﹣1）+ 
+2≥ 
+2，
当且仅当x﹣1= 时，取“=”号，
即x=1+ 
时，y有最小值2+ ．
故选：D．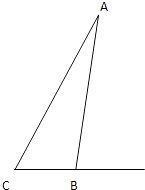
设BC的长度为x米，AC的长度为y米，依据题意可表示出AB的长度，然后代入到余弦定理中求得x和y的关系式，利用基本不等式求得y的最小值，并求得取等号时x的值．
练习册系列答案
相关题目
