题目内容
【题目】为创建全国文明城市,某区向各事业行政单位征集“文明过马路”义务督导员.从符合条件的600名志愿者中随机抽取100名,按年龄作分组如下:[20,25),[25,30),[30,35),[35,40),[40,45],并得到如下频率分布直方图.
(Ⅰ)求图中x的值,并根据频率分布直方图统计这600名志愿者中年龄在[30.40)的人数;
(Ⅱ)在抽取的100名志愿者中按年龄分层抽取10名参加区电视台“文明伴你行”节目录制,再从这10名志愿者中随机选取3名到现场分享劝导制止行人闯红灯的经历,记这3名志愿者中年龄不低于35岁的人数为X,求X的分布列及数学期望.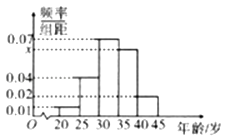
【答案】解:(Ⅰ)因为小矩形的面积等于频率.
所以(0.01+0.02+0.04+x+0,07)×5=1求得x=0.03.
所以这600名志愿者中,年龄在[30,40]人数为600×(0.07+0.05)×5=390(人).
(Ⅱ)用分层抽取的方法从中抽取10名志愿者,则年龄低于35岁的人数有100×(0.01+0.04+0.07)×5=6(人),
年龄不低于35岁的人数有100×(0.06+0.02)×5=4(人)
依题意,X的所有可能取值为0,1,2,3,则 ![]() ,
, ![]() .
.
所以X的分布列为
P | 0 | 1 | 2 | 3 |
X |
|
|
|
|
数学期望为 ![]()
【解析】(Ⅰ)由小矩形的面积等于频率.故面积和为1.即可求出x;(Ⅱ)用分层抽取的方法从中抽取10名志愿者,则年龄低于35岁的人数有6(人),年龄不低于35岁的人数有4(人),依题意,X的所有可能取值为0,1,2,3,求出相应的概率,即可.
【考点精析】本题主要考查了离散型随机变量及其分布列的相关知识点,需要掌握在射击、产品检验等例子中,对于随机变量X可能取的值,我们可以按一定次序一一列出,这样的随机变量叫做离散型随机变量.离散型随机变量的分布列:一般的,设离散型随机变量X可能取的值为x1,x2,.....,xi,......,xn,X取每一个值 xi(i=1,2,......)的概率P(ξ=xi)=Pi,则称表为离散型随机变量X 的概率分布,简称分布列才能正确解答此题.

【题目】如表提供了某厂节能降耗改造后在生产A产品过程中记录的产量x(吨)与相应的生产能耗y(吨)的几组对应数据,根据表中提供的数据,求出y关于x的线性回归方程为 ![]() =0.7x+0.35,则下列结论错误的是( )
=0.7x+0.35,则下列结论错误的是( )
x | 3 | 4 | 5 | 6 |
y | 2.5 | t | 4 | 4.5 |
A.线性回归直线一定过点(4.5,3.5)
B.产品的生产能耗与产量呈正相关
C.t的取值必定是3.15
D.A产品每多生产1吨,则相应的生产能耗约增加0.7吨
【题目】某重点中学为了解高一年级学生身体发育情况,对全校700名高一年级学生按性别进行分层抽样检查,测得身高(单位:cm)频数分布表如表1、表2. 表1:男生身高频数分布表
身高(cm) | [160,165) | [165,170) | [170,175) | [175,180) | [180,185) | [185,190) |
频数 | 2 | 5 | 14 | 13 | 4 | 2 |
表2:女生身高频数分布表
身高(cm) | [150,155) | [155,160) | [160,165) | [165,170) | [170,175) | [175,180) |
频数 | 1 | 7 | 12 | 6 | 3 | 1 |
(1)求该校高一女生的人数;
(2)估计该校学生身高在[165,180)的概率;
(3)以样本频率为概率,现从高一年级的男生和女生中分别选出1人,设X表示身高在[165,180)学生的人数,求X的分布列及数学期望.