题目内容
数列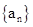 的前n项和
的前n项和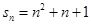 ;
;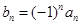 (n∈N*);则数列
(n∈N*);则数列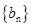 的前50项和为 ( )
的前50项和为 ( )
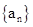 的前n项和
的前n项和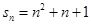 ;
;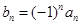 (n∈N*);则数列
(n∈N*);则数列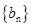 的前50项和为 ( )
的前50项和为 ( )| A.49 | B.50 | C.99 | D.100 |
A
解:∵数列{an}的前n项和Sn=n2+n+1,
∴a1=s1=3,当n≥2时,an=Sn -sn-1=n2+n+1-[(n-1)2+(n-1)+1]=2n,
故an=" 3" , n=1
2n , n≥2 .
∴bn=(-1)n an =" -" 3 , n="1"
(-1)n•2n , n≥2 ,
∴数列{bn}的前50项和为(-3+4)+(-6+8)+(-10+12)+…(-98+100)=1+24×2=49,
故选A.
∴a1=s1=3,当n≥2时,an=Sn -sn-1=n2+n+1-[(n-1)2+(n-1)+1]=2n,
故an=" 3" , n=1
2n , n≥2 .
∴bn=(-1)n an =" -" 3 , n="1"
(-1)n•2n , n≥2 ,
∴数列{bn}的前50项和为(-3+4)+(-6+8)+(-10+12)+…(-98+100)=1+24×2=49,
故选A.

练习册系列答案
相关题目
 满足
满足 ,
,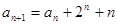
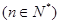 ,则
,则 =( )
=( )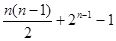
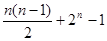


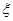 只能取三个值
只能取三个值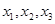 ,其概率依次成等差数列,则公差
,其概率依次成等差数列,则公差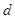 的取值范围为 .
的取值范围为 .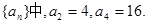
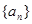 的通项公式;
的通项公式;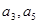 分别是等差数列
分别是等差数列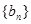 的第3项和第5项,求数列
的第3项和第5项,求数列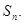
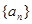 的前
的前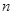 项和记为
项和记为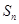 ,
,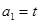 ,点
,点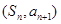 在直线
在直线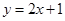 上,
上,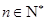 .
.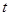 为何值时,数列
为何值时,数列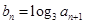 ,
,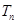 是数列
是数列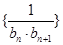 的前
的前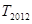 的值.
的值.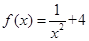 (x≠0),各项均为正数的数列
(x≠0),各项均为正数的数列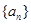 中
中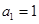 ,
,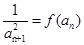 ,
,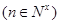 .
.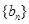 中,对任意的正整数
中,对任意的正整数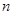 ,
, 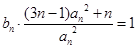 都成立,设
都成立,设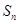 为数列
为数列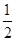 的大小.
的大小.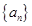 的前n项和为
的前n项和为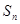 ,首项
,首项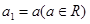 ,公差
,公差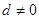 ,且
,且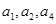 成等比数列。
成等比数列。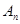 =
=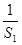 +
+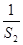 +
+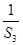 +…+
+…+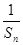 ,
, 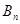 =
=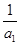 +
+ 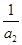 +
+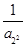 +… +
+… +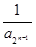 ,
,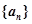 的各项均为正数,
的各项均为正数,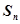 为其前
为其前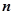 项和,对于任意
项和,对于任意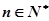 ,总有
,总有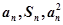 成等差数列.设数列
成等差数列.设数列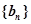 的前
的前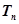 ,且
,且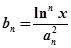 ,则对任意实数
,则对任意实数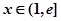 (
(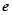 是常数,
是常数,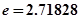 )和任意正整数
)和任意正整数