题目内容
(2008•湖北模拟)设 p:
(x,y∈R),q:x2+y2>r2(x,y∈R,r>0),若非q是非p的充分不必要条件,那么p是q的
|
充分非必要
充分非必要
条件,r的取值范围为(0,
]
| 12 |
| 5 |
(0,
]
.| 12 |
| 5 |
分析:由题意可得:非q⇒非p,而非q推不出非p,即可得到p⇒q,而q推不出p,进而得到答案;分别画出p与q表示的区域,再结合p是q的充分非必要,即可得到两个区域的关系,即圆的半径的最大值为:
=
,进而求出半径r的范围.
| 12 | ||
|
| 12 |
| 5 |
解答:解:因为非q是非p的充分必要条件,即非q⇒非p,而非q推不出非p,
所以p⇒q,而q推不出p,
所以p是q的充分非必要.
p:
(x,y∈R)表示的区域为图中阴影部分,
而q:x2+y2>r2(x,y∈R,r>0)表示图中圆的外面的部分(不包括圆周)
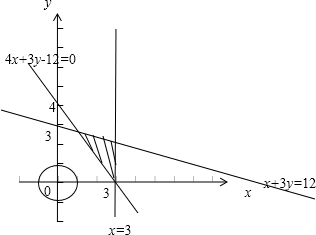
因为p是q的充分非必要,
所以阴影区域在圆的外面,即圆的半径的最大值为:
=
,
所以r的取值范围为:(0,
].
故答案为:充分非必要;(0,
].
所以p⇒q,而q推不出p,
所以p是q的充分非必要.
p:
|
而q:x2+y2>r2(x,y∈R,r>0)表示图中圆的外面的部分(不包括圆周)

因为p是q的充分非必要,
所以阴影区域在圆的外面,即圆的半径的最大值为:
| 12 | ||
|
| 12 |
| 5 |
所以r的取值范围为:(0,
| 12 |
| 5 |
故答案为:充分非必要;(0,
| 12 |
| 5 |
点评:本题主要考查必要条件、充分条件与充要条件的判断,以及平面区域的画法与点到直线的距离公式等知识点,此题综合性较强,属于中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 (2008•湖北模拟)已知向量
(2008•湖北模拟)已知向量