题目内容
 (2008•湖北模拟)已知向量
(2008•湖北模拟)已知向量| a |
| b |
| 2 |
| π |
| 2 |
| π |
| 2 |
| a |
| b |
(1)求函数f(x)的最大值,最小正周期;
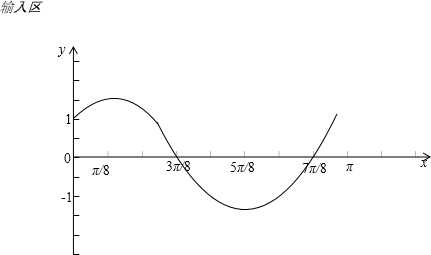
(2)作出函数f(x)在区间[0,π]上的图象.
分析:(1)由角α(α∈(-
,
))的终边上一点P(-t,-t)(t≠0),可得tanα=1,即α=
,进而得到f(x)=
sin(2x+
),再结合正弦函数的性质可得答案.
(2)首先根据x的范围求出2x+
的范围,再列表,进而结合五点作图法画出函数的图象.
| π |
| 2 |
| π |
| 2 |
| π |
| 4 |
| 2 |
| π |
| 4 |
(2)首先根据x的范围求出2x+
| π |
| 4 |
解答:解:(1)因为角α(α∈(-
,
))的终边上一点P(-t,-t)(t≠0)
所以tanα=1,
所以α=
,
所以f(x)=
•
=2
cosxsin(x+
)+tan(x+
)(x-
)
=2cosxsinx+2cos2x-1=sin2x+cos2x=
sin(2x+
)
所以f(x)的最大值为
,最小正周期T=π.
(2)列表:
所以f(x)=
sin(2x+
)的图象为:
| π |
| 2 |
| π |
| 2 |
所以tanα=1,
所以α=
| π |
| 4 |
所以f(x)=
| a |
| b |
| 2 |
| π |
| 4 |
| π |
| 4 |
| π |
| 4 |
=2cosxsinx+2cos2x-1=sin2x+cos2x=
| 2 |
| π |
| 4 |
所以f(x)的最大值为
| 2 |
(2)列表:
2x+
|
|
|
π |
|
2π |
| ||||||||||
| x | 0 |
|
|
|
|
π | ||||||||||
| y | 1 |
|
0 | -
|
0 | 1 |
| 2 |
| π |
| 4 |

点评:本题主要考查了利用二倍角的正弦余弦公式对三角函数式的化简,辅助角公式ainx+bcosx=
sin(x+θ)的运用,正弦函数的最值及周期性的求解,五点法作三角函数的图象,灵活运用三角函数的性质是解决本题的关键.
| a2+b2 |

练习册系列答案
 桃李文化快乐暑假武汉出版社系列答案
桃李文化快乐暑假武汉出版社系列答案 优秀生快乐假期每一天全新寒假作业本系列答案
优秀生快乐假期每一天全新寒假作业本系列答案 暑假接力赛新疆青少年出版社系列答案
暑假接力赛新疆青少年出版社系列答案
相关题目