题目内容
【题目】正方体ABCD﹣A1B1C1D1中,BB1与平面ACD1所成角的正弦值为( )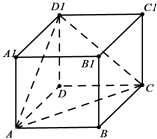
A.![]()
B.![]()
C.![]()
D.![]()
【答案】B
【解析】解:连接B1D,BD,则:AC⊥BD,
又AC⊥BB1 , ∴AC⊥平面BB1D,∴B1D⊥AC,
同理B1D⊥AD1 , ∴B1D⊥平面ACD1;
设B1D交平面ACD1于E,连接EA,EC,ED1 , B1D1 , B1A,B1C,
则容易证明△B1ED1 , △B1EC,△B1EA,三个三角形全等,
取CD1中点F,连接EF,则EF⊥CD1 , ![]() ,
,
设正方体的棱长为a,则 ![]() ,
, ![]() ,
, 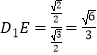 ;
;
通过前面知∠DD1E是DD1和平面ACD1所成的角,
又BB1∥DD1 ,
∴它也是BB1与平面ACD1所成角,则:
cos∠DD1E= ![]() ,
,
∴sin∠DD1E= ![]() .
.
故选B.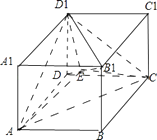
【考点精析】解答此题的关键在于理解空间角的异面直线所成的角的相关知识,掌握已知![]() 为两异面直线,A,C与B,D分别是
为两异面直线,A,C与B,D分别是![]() 上的任意两点,
上的任意两点,![]() 所成的角为
所成的角为![]() ,则
,则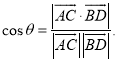 .
.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目