题目内容
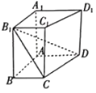
【题目】如图,三棱柱![]() 的底面是正三角形,
的底面是正三角形,![]() 底面
底面![]() ,M为
,M为![]() 的中点.
的中点.
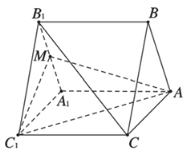
(1)求证:![]() 平面
平面![]() ;
;
(2)若![]() ,且沿侧棱
,且沿侧棱![]() 展开三棱柱的侧面,得到的侧面展开图的对角线长为
展开三棱柱的侧面,得到的侧面展开图的对角线长为![]() ,求作点
,求作点![]() 在平面
在平面![]() 内的射影H,请说明作法和理由,并求线段AH的长.
内的射影H,请说明作法和理由,并求线段AH的长.
【答案】(1)证明见解析(2)作法见解析,理由见解析,![]()
【解析】
(1)连结![]() ,交
,交![]() 于点O,连结OM,先证明
于点O,连结OM,先证明![]() ,进而得证;
,进而得证;
(2)过![]() 作
作![]() 于H,通过证明
于H,通过证明![]() 平面
平面![]() ,可得证;在
,可得证;在![]() 中,由射影定理,有
中,由射影定理,有![]() ,可计算得AH.
,可计算得AH.
(1)如图,
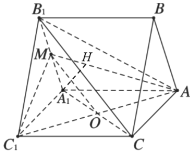
连结![]() ,交
,交![]() 于点O,连结OM.
于点O,连结OM.
因为三棱柱![]() 的侧面
的侧面![]() 是平行四边形,所以O为
是平行四边形,所以O为![]() 中点,
中点,
因为M为![]() 的中点,所以
的中点,所以![]() .
.
又因为![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
所以![]() 平面
平面![]() .
.
(2)过![]() 作
作![]() 于H,
于H,
因为![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,所以
,所以![]() ,
,
因为![]() 是正三角形,M为
是正三角形,M为![]() 的中点,
的中点,
所以![]() ,又
,又![]() ,
,![]()
![]() 平面
平面![]() ,
,
所以![]() 平面
平面![]() ,又
,又![]() 平面
平面![]() ,所以
,所以![]() ,
,
又因为![]() ,
,![]()
![]() 平面
平面![]() ,
,
所以![]() 平面
平面![]() 于H,
于H,
所以H为点![]() 在平面
在平面![]() 内的射影.
内的射影.
因为三棱柱侧面展开图是矩形,
且对角线长为![]() ,侧棱
,侧棱![]() ,
,
所以三棱柱底面周长为![]() .
.
又因为三棱柱的底面是正三角形,
所以底面边长![]()
![]() ,
,
在![]() 中,
中,![]()
![]() ,
,
由射影定理,有![]() ,
,
即![]() ,所以
,所以![]() .
.

 阅读快车系列答案
阅读快车系列答案【题目】某汽车品牌为了了解客户对于其旗下的五种型号汽车的满意情况,随机抽取了一些客户进行回访,调查结果如下表:
汽车型号 | I | II | III | IV | V |
回访客户(人数) | 250 | 100 | 200 | 700 | 350 |
满意率 | 0.5 | 0.3 | 0.6 | 0.3 | 0.2 |
满意率是指:某种型号汽车的回访客户中,满意人数与总人数的比值.
假设客户是否满意互相独立,且每种型号汽车客户对于此型号汽车满意的概率与表格中该型号汽车的满意率相等.
(1)从所有的回访客户中随机抽取1人,求这个客户满意的概率;
(2)从I型号和V型号汽车的所有客户中各随机抽取1人,设其中满意的人数为![]() ,求
,求![]() 的分布列和期望;
的分布列和期望;
(3)用 “![]() ”, “
”, “![]() ”, “
”, “![]() ”, “
”, “![]() ”, “
”, “![]() ”分别表示I, II, III, IV, V型号汽车让客户满意, “
”分别表示I, II, III, IV, V型号汽车让客户满意, “![]() ”, “
”, “![]() ”, “
”, “![]() ”, “
”, “![]() ”, “
”, “![]() ” 分别表示I, II, III, IV, V型号汽车让客户不满意.写出方差
” 分别表示I, II, III, IV, V型号汽车让客户不满意.写出方差![]() 的大小关系.
的大小关系.
【题目】某学校为了解学生的体育锻炼时间,采用简单随机抽样方法抽取了100名学生,对其平均每日参加体育锻炼的时间(单位:分钟)进行调查,按平均每日体育锻炼时间分组统计如下:
分组 |
|
|
|
|
|
|
男生人数 | 2 | 16 | 19 | 18 | 5 | 3 |
女生人数 | 3 | 20 | 10 | 2 | 1 | 1 |
若将平均每日参加体育锻炼的时间不低于120分钟的学生称为“锻炼达人”.
(1)将频率视为概率,估计该校4000名学生中“锻炼达人”有多少?
(2)从这100名学生的“锻炼达人”中按性别分层抽取5人参加某项体育活动.
①求男生和女生各抽取了多少人?
②若从这5人中随机抽取2人作为组长候选人,求抽取的2人中男女各1人的概率.