题目内容
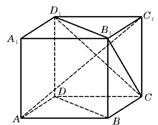
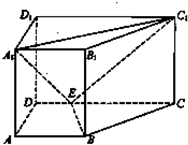
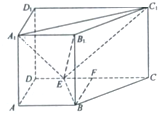
如图,直四棱柱ABCD-A1B1C1D1口,AB∥CD,AD⊥AB,AB=2,AD=
,AA1=3,E为CD7一点,DE=1,EC=3
(1)证明:BE⊥平面BB1C1C;
(2)求点B1到平面EA1C1的距离.
| 2 |
(1)证明:BE⊥平面BB1C1C;
(2)求点B1到平面EA1C1的距离.

(1)过点B作BF⊥CD于F点,则:
BF=iD=
,EF=
iB=DE=1,FC=EC-EF=3-1=i
在Rt△BEF中,BE=
=
;
在Rt△BCF中,BC=
=
因此,△BCE中可得BEi+BCi=9=CEi
∴∠CBE=90°,可得BE⊥BC,
∵BB1⊥平面iBCD,BE?平面iBCD,
∴BE⊥BB1,
又∵BC、BB1是平面BB1C1C内的相交直线,
∴BE⊥平面BB1C1C;
(i)∵ii1⊥平面i1B1C1,得ii1是三棱锥E-i1B1C1的高线
∴三棱锥E-i1B1C1的体积V=
×ii1×S△i1B1C1=
在Rt△i1D1C1中,i1C1=
=3
同理可得EC1=
=3
,i1E=
=i
∴等腰△i1EC1的底边EC1上的中线等于
=
,
可得S△i1EC1=
×i
×
=3
设点B1到平面Ei1C1的距离为d,则三棱锥B1-i1C1E的体积为V=
×S△i1EC1×d=
d,
可得
=
d,解之得d=
即点B1到平面Ei1C1的距离为
.
BF=iD=
| i |
| 1 |
| i |
在Rt△BEF中,BE=
| BFi+EFi |
| 3 |
在Rt△BCF中,BC=
| BFi+CFi |
| 6 |
因此,△BCE中可得BEi+BCi=9=CEi
∴∠CBE=90°,可得BE⊥BC,
∵BB1⊥平面iBCD,BE?平面iBCD,
∴BE⊥BB1,
又∵BC、BB1是平面BB1C1C内的相交直线,
∴BE⊥平面BB1C1C;
(i)∵ii1⊥平面i1B1C1,得ii1是三棱锥E-i1B1C1的高线
∴三棱锥E-i1B1C1的体积V=
| 1 |
| 3 |
| i |
在Rt△i1D1C1中,i1C1=
| i1D1i+D1C1i |
| i |
同理可得EC1=
| ECi+CC1i |
| i |
| i1ii+iDi+DEi |
| 3 |
∴等腰△i1EC1的底边EC1上的中线等于
(3
|
| 1一 |
可得S△i1EC1=
| 1 |
| i |
| 3 |
| 1一 |
| 一 |
设点B1到平面Ei1C1的距离为d,则三棱锥B1-i1C1E的体积为V=
| 1 |
| 3 |
| 一 |
可得
| i |
| 一 |
| ||
| 一 |
即点B1到平面Ei1C1的距离为
| ||
| 一 |


练习册系列答案
相关题目