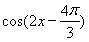题目内容
已知函数f(x)= +ln x.
+ln x.
(1)当a= 时,求f(x)在[1,e]上的最大值和最小值;
时,求f(x)在[1,e]上的最大值和最小值;
(2)若函数g(x)=f(x)- x在[1,e]上为增函数,求正实数a的取值范围.
x在[1,e]上为增函数,求正实数a的取值范围.
(1) 最大值是0,最小值是ln 2-1 (2)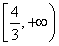
【解析】(1)当a=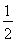 时,f(x)=
时,f(x)=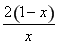 +ln x,
+ln x,
f′(x)=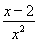 ,令f′(x)=0,得x=2.
,令f′(x)=0,得x=2.
∴当x∈[1,2)时,f′(x)<0,故f(x)在[1,2)上单调递减;
当x∈(2,e]时,f′(x)>0,故f(x)在(2,e]上单调递增.
∴f(x)在区间[1,e]上有唯一的极小值点,
故f(x)min=f(x)极小值=f(2)=ln 2-1.
又∵f(1)=0,f(e)=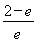 <0.
<0.
∴f(x)在区间[1,e]上的最大值f(x)max=f(1)=0.
综上可知,函数f(x)在[1,e]上的最大值是0,最小值是ln 2-1.
(2)∵g(x)=f(x)-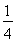 x=
x=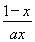 +ln x-
+ln x-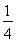 x,
x,
∴g′(x)=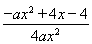 (a>0),
(a>0),
设φ(x)=-ax2+4ax-4,由题意知,只需φ(x)≥0在[1,e]上恒成立即可满足题意.
∵a>0,函数φ(x)的图象的对称轴为x=2,
∴只需φ(1)=3a-4≥0,即a≥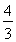 即可.
即可.
故正实数a的取值范围为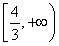 .
.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目