Question

设正实数x，y，z满足x2－3xy＋4y2－z＝0，则当取得最小值时，x＋2y－z的最大值为(　　)

A．0 B．

C．2 D．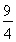

 

Answer 1

C

【解析】z＝x2－3xy＋4y2(x，y，z∈R＋)，

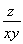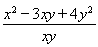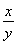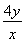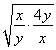∴＝＝＋－3≥2－3＝1.

当且仅当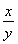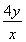＝，即x＝2y时“＝”成立，此时

z＝x2－3xy＋4y2＝4y2－6y2＋4y2＝2y2，

∴x＋2y－z＝2y＋2y－2y2＝－2y2＋4y＝－2(y－1)2＋2.

∴当y＝1时，x＋2y－z取最大值2.