题目内容
5.给定直线y=a与函数f(x)=x3-3x.(1)若直线y=a与f(x)的图象有且仅有两个交点,求实数a的值;
(2)若直线y=a与f(x)的图象有相异的三个交点,求实数a的取值范围.
分析 (1)先求出函数的导数,得到函数的单调区间,画出函数的图象,从而求出a的值;(2)结合函数的图象,从而求出a的范围即可.
解答 解:f′(x)=3(x+1)(x-1),
令f′(x)=0,得x1=1,x2=-1
当x变化时,f′(x),f(x)的变化情况如下表:
| x | (-∞,-1) | -1 | (-1,1) | 1 | (1,+∞) |
| f′(x) | + | 0 | - | 0 | + |
| f (x) | ↗ | 极大值2 | ↘ | 极小值-2 | ↗ |
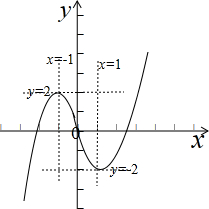 ,
,(1)当y=a经过极值点时有且仅有两个交点,此时a=±2.
(2)要使y=a与f (x)有三个不同的交点,由上图知a∈(-2,2).
点评 本小题主要考查导数概念及几何意义和用导数求函数的最值问题.

练习册系列答案
相关题目
10.下列属于相关现象的是( )
| A. | 利息与利率 | B. | 居民收入与储蓄存款 | ||
| C. | 电视机产量与苹果产量 | D. | 某同学学习成绩和体重 |
14.在等比数列{an}中,已知a1=1,a4=8,则a5=( )
| A. | 32 | B. | 32或-32 | C. | 16 | D. | 16或-16 |