题目内容
13.已知A(1,2),B(4,-2),在直线y=x-1上找一点P,使||PA|-|PB||最大,并求最大值.分析 求出点A关于x轴的对称点为A′,利用三角形两边之差小于第三边的思想,结合两点之间的距离公式进行求解即可.
解答 解:∵A﹙1,2﹚,B﹙4,-2﹚,在直线y=x-1的两侧,
∴作A﹙1,2﹚关于直线y=x-1的对称点A′
∵垂直于直线y=x-1且过点A﹙1,2﹚的直线方程设y=-x+b,
则由2=-1+b得b=3,
即方程为y=-x+3,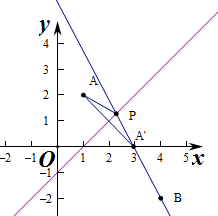
令y=0,得x=3,即A′(3,0).
∴由直线y=-x+3与直线y=x-1交点为(2,1),
∵过A′(3,0)和B﹙4,-2﹚的直线方程为$\frac{y-0}{-2-0}=\frac{x-3}{4-3}$,
即y=-2x+6,
∴由$\left\{\begin{array}{l}{y=-2x+6}\\{y=x-1}\end{array}\right.$,得$\left\{\begin{array}{l}{x=\frac{7}{3}}\\{y=\frac{4}{3}}\end{array}\right.$,即直线y=x-1与直线y=-2x+6的交点为P($\frac{7}{3}$,$\frac{4}{3}$),
此时||PA|-|PB||=||PA′|-|PB||≤|A′B|,
∵|A′B|=$\sqrt{(4-3)^{2}+(-2)^{2}}$=$\sqrt{1+4}$=$\sqrt{5}$,
∴当P的坐标为($\frac{7}{3}$,$\frac{4}{3}$)时,||PA|-|PB||有最大值$\sqrt{5}$.
点评 本题主要考查两点间的距离的问题,利用点的对称性转化为三点关系进行求解是解决本题的关键.

练习册系列答案
 能力评价系列答案
能力评价系列答案 唐印文化课时测评系列答案
唐印文化课时测评系列答案 导学与测试系列答案
导学与测试系列答案
相关题目
4.在△ABC中,a=4,A=30°,B=60°,则b等于( )
| A. | $4\sqrt{3}$ | B. | 6 | C. | $\sqrt{3}$ | D. | 9 |
8.z=$\frac{{{{({-1+\sqrt{3}i})}^3}}}{2^3}+\frac{{-1+\sqrt{2}i}}{{\sqrt{2}+i}}$,则|z|=( )
| A. | 2 | B. | $\sqrt{2}$ | C. | $\sqrt{5}$ | D. | 1 |