Question

15．已知△ABC中，A，B，C所对边长分别为a，b，c，且|a-b|=8，c=10，记O为AB的中点，则∠BOC的取值范围是（0，arctan$\frac{3}{4}$）∪（π-arctan$\frac{3}{4}$，π）．

Answer 1

分析 以AB的中点为坐标原点，AB所在直线为x轴，建立坐标系，设C（x，y），由||CB|-|CA||=8＜|AB|=10，由双曲线的定义可知C在双曲线上运动，求出渐近线方程，可得斜率，通过图形观察，即可得到直线OC的斜率范围，进而得到所求角的范围．

解答 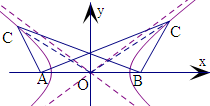解：以AB的中点为坐标原点，
AB所在直线为x轴，建立坐标系，
设C（x，y），由||CB|-|CA||=8＜|AB|=10，
可知C点在以A（-5，0），B（5，0）为焦点的双曲线上，
且有双曲线的实轴长为8，虚轴长为9，
则双曲线的方程为$\frac{{x}^{2}}{16}$-$\frac{{y}^{2}}{9}$=1．
双曲线的渐近线方程为y=±$\frac{3}{4}$x，
若C在双曲线右支上，直线OC的斜率范围是（0，$\frac{3}{4}$），
若C在双曲线左支上，直线OC的斜率范围是（-$\frac{3}{4}$，0），
则∠BOC的取值范围是（0，arctan$\frac{3}{4}$）∪（π-arctan$\frac{3}{4}$，π）．
故答案为：（0，arctan$\frac{3}{4}$）∪（π-arctan$\frac{3}{4}$，π）．

点评 本题考查三角形中角的范围的求法，考查双曲线的定义和方程及性质：渐近线的运用，运用数形结合的思想方法是解题的关键．