题目内容
若x的方程x2-x+a=0和x2-x+b=0(a≠b)的四个根可组成首项为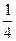 的等差数列,则a+b的值为( )
的等差数列,则a+b的值为( )
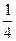 的等差数列,则a+b的值为( )
的等差数列,则a+b的值为( )A.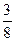 | B.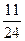 | C.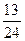 | D.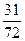 |
D
x2-x+a=0和x2-x+b=0各有两根,且这两个方程的两根和都等于1,且四个根组成等差数列,
所以可设四个根为a1,a2,a3,a4.根据等差数列的性质,只能a1+a4=a2+a3=1,设公差为d,
则a1+a4=2a1+3d=2×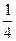 +3d=1.
+3d=1.
∴d=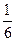 .
.
从而a2=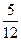 ,a3=
,a3=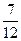 ,a4=
,a4=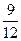 ,
,
于是a+b=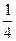 ×
×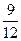 +
+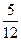 ×
×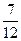 =
=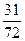 .
.
故选D.
所以可设四个根为a1,a2,a3,a4.根据等差数列的性质,只能a1+a4=a2+a3=1,设公差为d,
则a1+a4=2a1+3d=2×
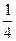 +3d=1.
+3d=1.∴d=
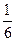 .
.从而a2=
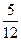 ,a3=
,a3=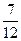 ,a4=
,a4=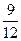 ,
,于是a+b=
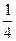 ×
×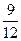 +
+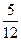 ×
×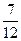 =
=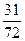 .
.故选D.

练习册系列答案
 全优考典单元检测卷及归类总复习系列答案
全优考典单元检测卷及归类总复习系列答案
相关题目
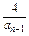 (n≥2),令bn=
(n≥2),令bn=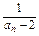 .求证:数列{bn}是等差数列.
.求证:数列{bn}是等差数列. 为整数,集合
为整数,集合 中的数由小到大组成数列
中的数由小到大组成数列 :
: ,则
,则 。
。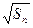 =an+1.
=an+1.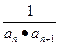 ,求数列{bn}的前n项和Bn.
,求数列{bn}的前n项和Bn.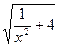 (x>0),数列{an}中,a1=1,
(x>0),数列{an}中,a1=1,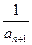 =-f(an),求数列{an}的通项公式.
=-f(an),求数列{an}的通项公式. 中,前
中,前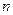 项和为
项和为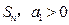 ,且
,且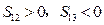 .则
.则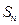 最大?
最大?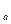 !=(n
!=(n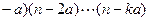 ,其中k是满足n>ka的最大整数,那么
,其中k是满足n>ka的最大整数,那么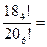 _________
_________