题目内容
已知函数f(x)=-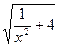 (x>0),数列{an}中,a1=1,
(x>0),数列{an}中,a1=1,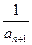 =-f(an),求数列{an}的通项公式.
=-f(an),求数列{an}的通项公式.
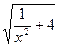 (x>0),数列{an}中,a1=1,
(x>0),数列{an}中,a1=1,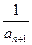 =-f(an),求数列{an}的通项公式.
=-f(an),求数列{an}的通项公式.an=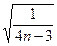 .
.
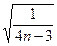 .
.∵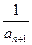 =-f(an),
=-f(an),
∴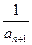 =-
=-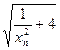 .
.
∴ =
=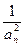 +4.
+4.
∴ -
-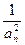 =4.
=4.
则{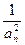 }是以
}是以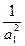 =1为首项,4为公差的等差数列.
=1为首项,4为公差的等差数列.
∴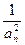 =1+4(n-1)=4n-3.
=1+4(n-1)=4n-3.
∴an2=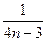 .
.
∵an>0,
∴an=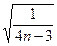 .
.
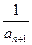 =-f(an),
=-f(an),∴
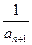 =-
=-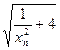 .
.∴
 =
=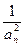 +4.
+4.∴
 -
-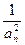 =4.
=4.则{
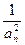 }是以
}是以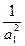 =1为首项,4为公差的等差数列.
=1为首项,4为公差的等差数列.∴
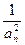 =1+4(n-1)=4n-3.
=1+4(n-1)=4n-3.∴an2=
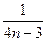 .
.∵an>0,
∴an=
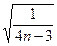 .
.
练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
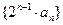 的前n项和Sn=9-6n.
的前n项和Sn=9-6n. 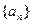 的通项公式.
的通项公式.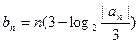 ,求数列
,求数列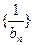 的前n项和.
的前n项和.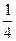 的等差数列,则a+b的值为( )
的等差数列,则a+b的值为( )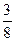
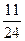
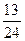
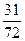
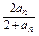 ,n∈N*,猜想这个数列的通项公式是什么?这个猜想正确吗?说明理由.
,n∈N*,猜想这个数列的通项公式是什么?这个猜想正确吗?说明理由. ,
, ,
,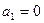 ,
,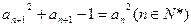 .记:
.记: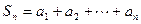
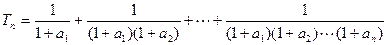 .
.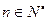 时,
时,  ;
;  ;
;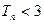 。
。