题目内容
(本小题满分14分)
在数列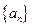 中,
中,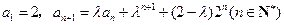 ,其中
,其中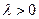 .
.
(Ⅰ)求数列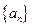 的通项公式;
的通项公式;
(Ⅱ)求数列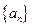 的前
的前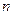 项和
项和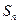 ;
;
(Ⅲ)证明存在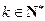 ,使得
,使得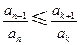 对任意
对任意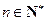 均成立.
均成立.
在数列
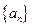 中,
中,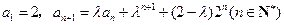 ,其中
,其中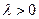 .
.(Ⅰ)求数列
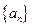 的通项公式;
的通项公式;(Ⅱ)求数列
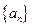 的前
的前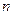 项和
项和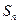 ;
;(Ⅲ)证明存在
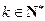 ,使得
,使得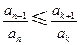 对任意
对任意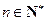 均成立.
均成立.(Ⅰ)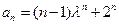
(Ⅱ)当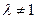 时,①式减去②式,数列
时,①式减去②式,数列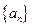 的前
的前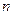 项和
项和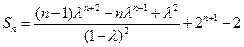
当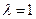 时,
时,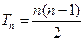 .这时数列
.这时数列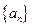 的前
的前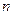 项和
项和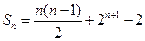
(Ⅲ)存在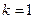 ,使得
,使得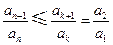 对任意
对任意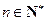 均成立。
均成立。
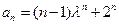
(Ⅱ)当
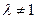 时,①式减去②式,数列
时,①式减去②式,数列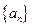 的前
的前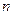 项和
项和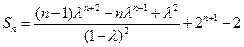
当
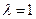 时,
时,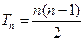 .这时数列
.这时数列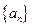 的前
的前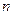 项和
项和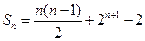
(Ⅲ)存在
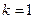 ,使得
,使得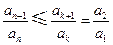 对任意
对任意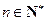 均成立。
均成立。(Ⅰ)解法一: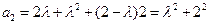 ,
,
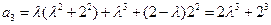 ,
,
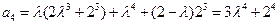 .
.
由此可猜想出数列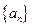 的通项公式为
的通项公式为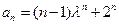 .
.
以下用数学归纳法证明.
(1)当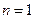 时,
时,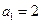 ,等式成立.
,等式成立.
(2)假设当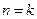 时等式成立,即
时等式成立,即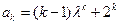 ,
,
那么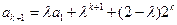
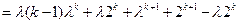
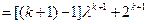 .
.
这就是说,当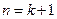 时等式也成立.根据(1)和(2)可知,等式
时等式也成立.根据(1)和(2)可知,等式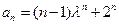 对任何
对任何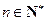 都成立.
都成立.
解法二:由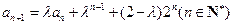 ,
,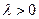 ,
,
可得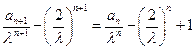 ,
,
所以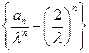 为等差数列,其公差为1,首项为0,故
为等差数列,其公差为1,首项为0,故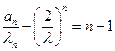 ,所以数列
,所以数列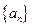 的通项公式为
的通项公式为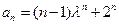 .
.
(Ⅱ)解:设 , ①
, ①
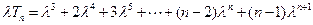 ②
②
当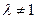 时,①式减去②式,
时,①式减去②式,
得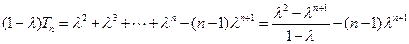 ,
,
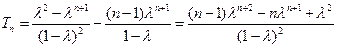 .
.
这时数列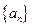 的前
的前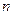 项和
项和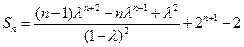 .
.
当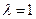 时,
时,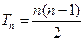 .这时数列
.这时数列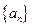 的前
的前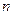 项和
项和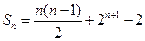 .
.
(Ⅲ)证明:通过分析,推测数列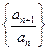 的第一项
的第一项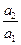 最大,下面证明:
最大,下面证明:
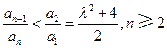 . ③
. ③
由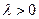 知
知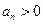 ,要使③式成立,只要
,要使③式成立,只要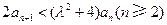 ,
,
因为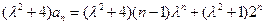
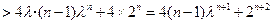
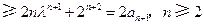 .
.
所以③式成立.
因此,存在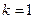 ,使得
,使得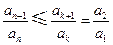 对任意
对任意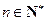 均成立.
均成立.
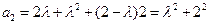 ,
,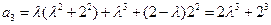 ,
,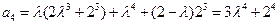 .
.由此可猜想出数列
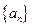 的通项公式为
的通项公式为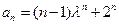 .
.以下用数学归纳法证明.
(1)当
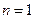 时,
时,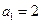 ,等式成立.
,等式成立.(2)假设当
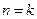 时等式成立,即
时等式成立,即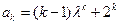 ,
,那么
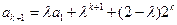
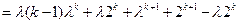
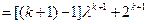 .
.这就是说,当
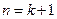 时等式也成立.根据(1)和(2)可知,等式
时等式也成立.根据(1)和(2)可知,等式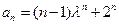 对任何
对任何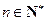 都成立.
都成立.解法二:由
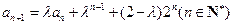 ,
,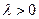 ,
,可得
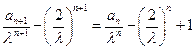 ,
,所以
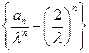 为等差数列,其公差为1,首项为0,故
为等差数列,其公差为1,首项为0,故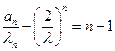 ,所以数列
,所以数列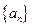 的通项公式为
的通项公式为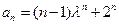 .
.(Ⅱ)解:设
 , ①
, ①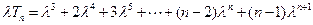 ②
②当
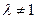 时,①式减去②式,
时,①式减去②式,得
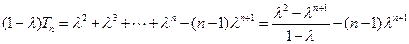 ,
,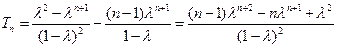 .
.这时数列
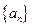 的前
的前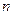 项和
项和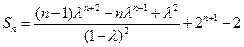 .
.当
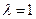 时,
时,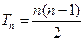 .这时数列
.这时数列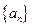 的前
的前 项和
项和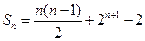 .
.(Ⅲ)证明:通过分析,推测数列
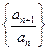 的第一项
的第一项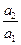 最大,下面证明:
最大,下面证明: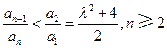 . ③
. ③由
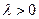 知
知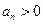 ,要使③式成立,只要
,要使③式成立,只要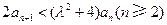 ,
,因为
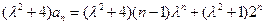
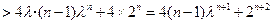
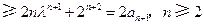 .
.所以③式成立.
因此,存在
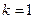 ,使得
,使得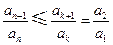 对任意
对任意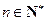 均成立.
均成立.
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
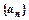 中,
中,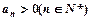 ,公比
,公比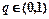 ,且
,且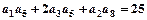 ,又
,又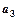 与
与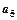 的等比中项为
的等比中项为 ,
,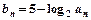 ,数列
,数列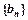 的前
的前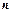 项和为
项和为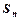 ,求数列
,求数列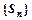 的通项公式
的通项公式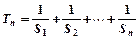 ,求
,求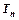
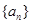 ,
,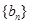 与函数
与函数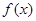 ,
,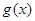 ,
,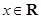 满足条件:
满足条件: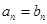 ,
,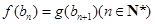 .
.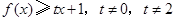 ,
,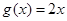 ,
,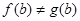 ,
,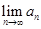 存在,求
存在,求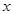 的取值范围;
的取值范围;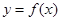 为
为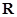 上的增函数,
上的增函数,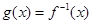 ,
,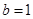 ,
,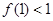 ,证明对任意
,证明对任意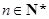 ,
,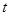 表示).
表示).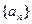 是首项
是首项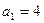 的等比数列,其前
的等比数列,其前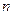 项和为Sn,且
项和为Sn,且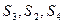 成等比数列.
成等比数列.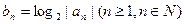 ,设
,设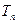 为数列
为数列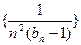 的前
的前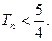
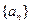 满足
满足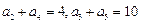 ,则它的前10
,则它的前10 项和
项和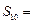 ( )
( ) 

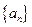 的前
的前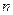 项和
项和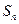 满足
满足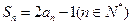 ,那么数列
,那么数列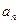 = .
= .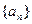 中,
中,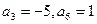 ,此数列的通项公式为 ,设
,此数列的通项公式为 ,设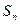 是数列
是数列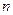 项和,则
项和,则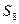 等于 。
等于 。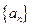 中,
中, 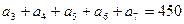 ,则
,则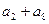 等于 ( )
等于 ( )