题目内容
设数列{an}共有n( )项,且
)项,且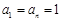 ,对每个i (1≤i≤
,对每个i (1≤i≤ ,i
,i N),均有
N),均有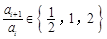 .
.
(1)当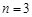 时,写出满足条件的所有数列{an}(不必写出过程);
时,写出满足条件的所有数列{an}(不必写出过程);
(2)当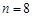 时,求满足条件的数列{an}的个数.
时,求满足条件的数列{an}的个数.
(1)共有3个: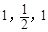 ; 1,1,1; 1,2,1;(2)数列{an}的个数为393.
; 1,1,1; 1,2,1;(2)数列{an}的个数为393.
解析试题分析:(1)根据题意可得当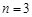 时,有
时,有 ,因为题中要求
,因为题中要求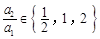 ,
,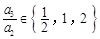 ,也就是说
,也就是说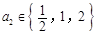 ,
,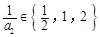 ,这样即可得
,这样即可得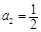 或
或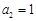 或
或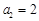 ,故此时满足条件的数列{an}共有3个:
,故此时满足条件的数列{an}共有3个: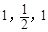 ; 1,1,1; 1,2,1;(2)由题中要求可联想到令bi=
; 1,1,1; 1,2,1;(2)由题中要求可联想到令bi=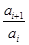 (1≤i≤7),则对每个符合条件的数列{an},满足条件:
(1≤i≤7),则对每个符合条件的数列{an},满足条件: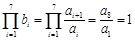 ,且bi∈
,且bi∈ (1≤i≤7),则此时可设符合条件的数列{bn}的个数为N, bi (1≤i≤7)中有k个2;从而有k个
(1≤i≤7),则此时可设符合条件的数列{bn}的个数为N, bi (1≤i≤7)中有k个2;从而有k个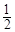 ,7-2k个1,当k给定时,{bn}的取法有
,7-2k个1,当k给定时,{bn}的取法有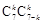 种,故此时
种,故此时 .
.
试题解析:(1)当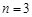 时,
时, .
.
因为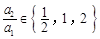 ,
,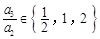 ,即
,即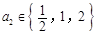 ,
,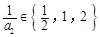 ,
,
所以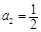 或
或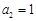 或
或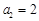 .
.
故此时满足条件的数列{an}共有3个: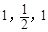 ; 1,1,1; 1,2,1. 3分
; 1,1,1; 1,2,1. 3分
(2)令bi=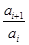 (1≤i≤7),则对每个符合条件的数列{an},满足条件:
(1≤i≤7),则对每个符合条件的数列{an},满足条件: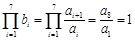 ,且bi∈
,且bi∈ (1≤i≤7).
(1≤i≤7).
反之,由符合上述条件的7项数列{bn}可唯一确定一个符合条件的8项数列{an}. 7分
记符合条件的数列{bn}的个数为N.
显然,bi (1≤i≤7)中有k个2;从而有k个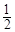 ,7-2k个1.
,7-2k个1.
当k给定时,{bn}的取法有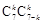 种,易得k的可能值只有0,1,2,3,
种,易得k的可能值只有0,1,2,3,
故 .
.
因此,符合条件的数列{an}的个数为393. 10分
考点:1.数列的递推关系;2.排列组合的应用;3.代数式的处理

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 满足对任意的
满足对任意的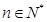 ,都有
,都有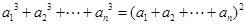 且
且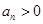 .
.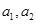 的值;
的值;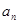 ;
;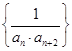 的前
的前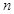 项和为
项和为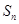 ,不等式
,不等式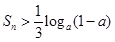 对任意的正整数
对任意的正整数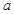 的取值范围.
的取值范围.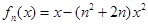 (其中
(其中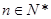 ),区间
),区间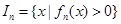 .
. 的长度(注:区间
的长度(注:区间 的长度定义为
的长度定义为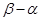 );
);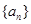 ,令
,令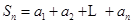 ,证明:
,证明: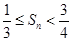 .
.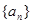 的首项
的首项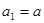 ,
,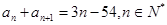
 项和为
项和为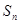 ,若
,若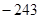 ,求
,求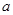 的取值范围?
的取值范围?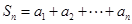 ,
, ,且
,且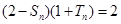 ,
, .
.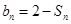 ,证明数列{bn}是等比数列;
,证明数列{bn}是等比数列;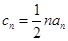 ,求集合
,求集合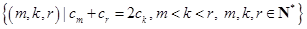 .
.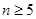 ):第一行是以4为首项,4为公差的等差数列,从第二行起,每一个数是其肩上两个数的和,例如:
):第一行是以4为首项,4为公差的等差数列,从第二行起,每一个数是其肩上两个数的和,例如: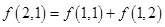 ;
;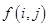 为数表中第
为数表中第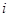 行的第
行的第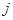 个数.
个数.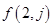 和
和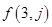 ;
;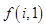 关于
关于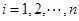 )的表达式.
)的表达式.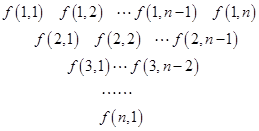
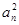 ·bn,证明:当且仅当n≥3时,cn+1<cn..
·bn,证明:当且仅当n≥3时,cn+1<cn..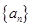 的前
的前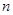 项和为
项和为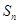 ,
,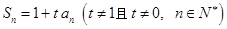 .
. ,求实数
,求实数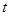 的取值范围.
的取值范围.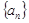 满足
满足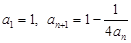 ,其中
,其中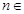 N*.
N*.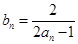 ,求证:数列
,求证:数列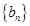 是等差数列,并求出
是等差数列,并求出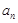 ;
;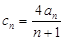 ,数列
,数列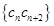 的前
的前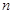 项和为
项和为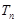 ,是否存在正整数
,是否存在正整数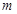 ,使得
,使得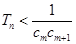 对于
对于