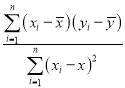题目内容
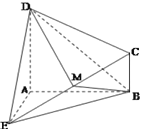
【题目】如图,已知椭圆![]() 的左、右焦点分别为
的左、右焦点分别为![]() 、
、![]() ,点
,点![]() 为椭圆
为椭圆![]() 上任意一点,
上任意一点,![]() 关于原点
关于原点![]() 的对称点为
的对称点为![]() ,有
,有![]() ,且
,且![]() 的最大值
的最大值![]() .
.

(1)求椭圆![]() 的标准方程;
的标准方程;
(2)若![]() 是
是![]() 关于
关于![]() 轴的对称点,设点
轴的对称点,设点![]() ,连接
,连接![]() 与椭圆
与椭圆![]() 相交于点
相交于点![]() ,问直线
,问直线![]() 与
与![]() 轴是否交于一定点.如果是,求出该定点坐标;如果不是,说明理由.
轴是否交于一定点.如果是,求出该定点坐标;如果不是,说明理由.
【答案】(1)![]() ;(2)定点
;(2)定点![]() .
.
【解析】
(1)由对称可得![]() ,故
,故![]() .又根据
.又根据![]() 的最大值
的最大值![]() 得到
得到![]() ,进而得到
,进而得到![]() ,
,![]() ,所以可得到椭圆的方程.
,所以可得到椭圆的方程.
(2)由题意可设直线![]() 的方程为
的方程为![]() ,结合由直线方程与椭圆方程组成的方程组可得直线
,结合由直线方程与椭圆方程组成的方程组可得直线![]() 的方程为
的方程为![]() ,令
,令![]() 得
得![]() ,将
,将![]() ,
,![]() 代入上式整理得
代入上式整理得![]() ,然后代入两根和与两根积可得
,然后代入两根和与两根积可得![]() ,从而得直线
,从而得直线![]() 与
与![]() 轴交于定点
轴交于定点![]() .
.
(1)因为点![]() 为椭圆上任意一点,
为椭圆上任意一点,![]() 关于原点
关于原点![]() 的对称点为
的对称点为![]() ,
,
所以![]() ,
,
又![]() ,
,
所以![]() ,
,
![]() .
.
又![]() 的最大值为
的最大值为![]() ,知当
,知当![]() 为上顶点时,
为上顶点时,![]() 最大,
最大,
所以![]() ,
,
所以![]() ,
,
所以![]() .
.
所以椭圆![]() 的标准方程为
的标准方程为![]() .
.
(2)由题知直线![]() 的斜率存在,设直线
的斜率存在,设直线![]() 的方程为
的方程为![]() .
.
由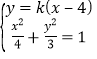 消去
消去![]() 并整理得
并整理得![]() .
.
因为直线![]() 与椭圆交于
与椭圆交于![]() 两点,
两点,
所以![]() ,
,
解得![]() .
.
设![]() ,
,![]() ,则
,则![]() ,
,
且![]() ,
,![]() ,①
,①
由题意得,直线![]() 的方程为
的方程为![]() ,
,
令![]() 得
得![]() ,
,
将![]() ,
,![]() 代入上式整理得
代入上式整理得![]() .
.
将①代入上式,得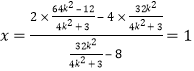 ,
,
所以直线![]() 与
与![]() 轴交于定点
轴交于定点![]() .
.

练习册系列答案
 小学期末标准试卷系列答案
小学期末标准试卷系列答案
相关题目
【题目】对某校高一年级学生参加社区服务次数进行统计,随机抽取M名学生作为样本,得到这M名学生参加社区服务的次数.根据此数据作出了频数与频率的统计表和频率分布直方图如下:
分组 | 频数 | 频率 |
[10,15) | 10 | 0.25 |
[15,20) | 25 | n |
[20,25) | m | p |
[25,30) | 2 | 0.05 |
合计 | M | 1 |
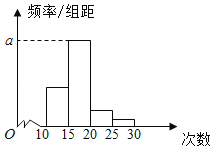
(1)求出表中M,p及图中a的值;
(2)若该校高一学生有360人,试估计该校高一学生参加社区服务的次数在区间[15,20)内的人数;
(3)在所取样本中,从参加社区服务的次数不少于20次的学生中任选2人,请列举出所有基本事件,并求至多1人参加社区服务次数在区间[20,25)内的概率.