题目内容
【题目】已知函数![]() .
.
(1)讨论![]() 的单调性;
的单调性;
(2)当![]() 时,
时,![]() ,求
,求![]() 的最大整数值.
的最大整数值.
【答案】(1)![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单调递增.(2)2.
上单调递增.(2)2.
【解析】
分析:(1)先确定函数![]() 的定义域,再求出函数
的定义域,再求出函数![]() 的导数,
的导数,![]()
![]() , 分类讨论,确定
, 分类讨论,确定![]() 和
和![]() 时函数的单调性.
时函数的单调性.
(2)根据题意,转化为![]() 时,
时,![]() 条件下求参数问题.由(1)可知:①当
条件下求参数问题.由(1)可知:①当![]() 时
时![]() 在
在![]() 上单调递增,且
上单调递增,且![]() ,即
,即![]() 成立;②
成立;②![]() 时,即
时,即![]() ,分析情况同①;③
,分析情况同①;③![]() 时,即
时,即![]() ,
,![]() ,构造关于
,构造关于![]() 的新函数
的新函数![]() ,判断函数的单调性,确定函数零点位置
,判断函数的单调性,确定函数零点位置![]() ,而
,而![]() ;综上得
;综上得![]() 的最大整数值为
的最大整数值为![]() .
.
详解:解:(1)函数![]() 的定义域为
的定义域为![]() .
.
![]()
![]()
![]() ,
,
当![]() 时,
时,![]() ,
,![]() 在
在![]() 上单调递增,
上单调递增,
当![]() 时,令
时,令![]() ,得
,得![]() ,令
,令![]() ,得
,得![]() ,
,
![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单调递增.
上单调递增.
(2)由(1)知,当![]() 时
时![]() 在
在![]() 上单调递增,
上单调递增,
又![]() ,所以当
,所以当![]() 时,
时,![]() ,满足题意.
,满足题意.
由(1)知,当![]() 时,
时,![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单调递增.
上单调递增.
若![]() ,即
,即![]() ,
,![]() 在
在![]() 上单调递增,
上单调递增,
所以当![]() 时,
时,![]() ,满足题意.
,满足题意.
若![]() ,即
,即![]() ,
,![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单调递增.
上单调递增.
![]()
![]()
![]() 即
即![]()
![]()
令![]() ,
,
![]() ,
,
![]() 在
在![]() 上单调递减,
上单调递减,
又![]() ,
,![]() ,
,
![]() 在
在![]() 上存在唯一零点
上存在唯一零点![]() ,
,
![]()
![]()
综上所述,![]() 的取值范围为
的取值范围为![]() ,故
,故![]() 的最大整数值为
的最大整数值为![]() .
.

 阅读快车系列答案
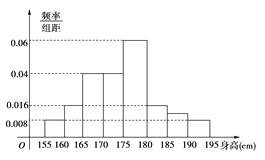
阅读快车系列答案【题目】东莞市摄影协会准备在2019年10月举办主题为“庆祖国70华诞——我们都是追梦人”摄影图片展.通过平常人的镜头记录国强民富的幸福生活,向祖国母亲的生日献礼,摄影协会收到了来自社会各界的大量作品,打算从众多照片中选取100张照片展出,其参赛者年龄集中在![]() 之间,根据统计结果,做出频率分布直方图如图:
之间,根据统计结果,做出频率分布直方图如图:

(1)求频率分布直方图中![]() 的值,并根据频率分布直方图,求这100位摄影者年龄的样本平均数
的值,并根据频率分布直方图,求这100位摄影者年龄的样本平均数![]() 和中位数
和中位数![]() (同一组数据用该区间的中点值作代表);
(同一组数据用该区间的中点值作代表);
(2)为了展示不同年龄作者眼中的祖国形象,摄影协会按照分层抽样的方法,计划从这100件照片中抽出20个最佳作品,并邀请相应作者参加“讲述照片背后的故事”座谈会.
①在答题卡上的统计表中填出每组相应抽取的人数:
年龄 |
|
|
|
|
|
人数 |
②若从年龄在![]() 的作者中选出2人把这些图片和故事整理成册,求这2人至少有一人的年龄在
的作者中选出2人把这些图片和故事整理成册,求这2人至少有一人的年龄在![]() 的概率.
的概率.
【题目】某书店刚刚上市了《中国古代数学史》,销售前该书店拟定了5种单价进行试销,每种单价(![]() 元)试销l天,得到如表单价
元)试销l天,得到如表单价![]() (元)与销量
(元)与销量![]() (册)数据:
(册)数据:
单价 | 18 | 19 | 20 | 21 | 22 |
销量 | 61 | 56 | 50 | 48 | 45 |
(l)根据表中数据,请建立![]() 关于
关于![]() 的回归直线方程:
的回归直线方程:
(2)预计今后的销售中,销量![]() (册)与单价
(册)与单价![]() (元)服从(l)中的回归方程,已知每册书的成本是12元,书店为了获得最大利润,该册书的单价应定为多少元?
(元)服从(l)中的回归方程,已知每册书的成本是12元,书店为了获得最大利润,该册书的单价应定为多少元?
附: ,
,![]() ,
,![]() ,
,![]() .
.
【题目】为了解甲、乙两奶粉厂的产品质量,采用分层抽样的方法从甲、乙两奶粉厂生产的产品中分别抽取16件和5件,测量产品中微量元素![]() 的含量(单位:毫克).下表是乙厂的5件产品的测量数据:
的含量(单位:毫克).下表是乙厂的5件产品的测量数据:
编号 | 1 | 2 | 3 | 4 | 5 |
| 170 | 178 | 166 | 176 | 180 |
| 74 | 80 | 77 | 76 | 81 |
(1)已知甲厂生产的产品共有96件,求乙厂生产的产品数量;
(2)当产品中的微量元素![]() 满足
满足![]() 且
且![]() 时,该产品为优等品.用上述样本数据估计乙厂生产的优等品的数量;
时,该产品为优等品.用上述样本数据估计乙厂生产的优等品的数量;
(3)从乙厂抽出的上述5件产品中,随机抽取2件,求抽取的2件产品中优等品数![]() 的分布列及其均值(即数学期望).
的分布列及其均值(即数学期望).