题目内容
【题目】已知椭圆C： 
+ 
=1（a＞b＞0）的左、右焦点分别为F1、F2 ， 点M（0，2）关于直线y=﹣x的对称点在椭圆C上，且△MF1F2为正三角形．
（1）求椭圆C的方程；
（2）垂直于x轴的直线与椭圆C交于A，B两点，过点P（4，0）的直线PB交椭圆C于另一点E，证明：直线AE与x轴相交于定点．
【答案】
（1）解：如图，点M（0，2）关于直线y=﹣x的对称点为（﹣2，0），
∵（﹣2，0）在椭圆上，∴a=2，
又△MF1F2为正三角形，
∴tan30°= 
，c=2tan30°= 
，
∴b2=a2﹣c2=4﹣ 
= 
，
∴椭圆C的方程 
+ 
=1；
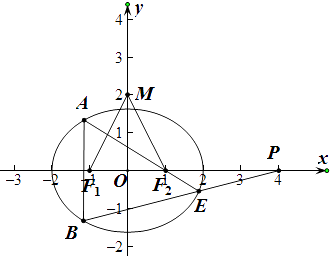
（2）解：∵P（4，0），
∴直线PB的方程可设为x=ky+4，
由 
，
得（2k2+3）y2+16ky+24=0，
∵△＞0，
∴k2＞ 
．
设B（x1，y1），E（x2，y2），则A（x1，﹣y1），
∴y1+y2=﹣ 
，y1y2= 
直线AE：y+y1= 
（x﹣x1），
∵x1y2+x2y1=2ky1y2+4（y1+y2）= 
﹣ 
=﹣ =y1+y2，
∴直线AE：y+y1= （x﹣x1），即为y= （x﹣1）恒过定点（1，0）．
∴AE恒过定点（1，0）．
【解析】（1）由题意画出图形，求出M点关于直线y=﹣x的对称点，则a可求，再由△MF1F2为正三角形列式求得c，结合隐含条件求得b，则椭圆方程可求，（2）设直线PB的方程可设为x=ky+4，联立方程组，设B（x1 ， y1），E（x2 ， y2），则A（x1 ， ﹣y1），根据韦达定理可得y1+y2=﹣ ，y1y2= ，由此能够证明直线AE恒过定点（1，0）．
【考点精析】本题主要考查了椭圆的标准方程的相关知识点，需要掌握椭圆标准方程焦点在x轴：
，焦点在y轴：
才能正确解答此题．
