题目内容
【题目】已知点P（0，2）和圆C：x2+y2﹣8x+11=0．
（1）求过点P，点C和原点三点圆的方程；
（2）求以点P为圆心且与圆C外切的圆的方程．
【答案】
（1）解：化圆C：x2+y2﹣8x+11=0为（x﹣4）2+y2=5，
则圆心C（4，0），半径r= 
，
设过点P，点C和原点三点圆的方程为x2+y2+Dx+Ey+F=0．
代入点的坐标得： 
，即 
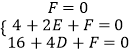，解得：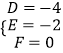 
．
∴过点P，点C和原点三点圆的方程为x2+y2﹣4x﹣2y=0；
（2）解：如图，∵C（4，0），P（0，2），
∴|PC|= 
，
又圆C的半径r= ，且圆P与圆C外切，
∴圆P的半径为 
．
则以点P为圆心且与圆C外切的圆的方程为x2+（y﹣2）2=5．
【解析】（1）化圆C的方程为标准方程，求出圆C的圆心坐标和半径，再设过点P，点C和原点三点圆的方程为x2+y2+Dx+Ey+F=0．代入点的坐标可得关于D、E、F的三元一次方程组，求出D、E、F的值得所求圆的方程；（2）求出P与C的距离，减去已知圆的半径得到要求圆的半径，代入圆的标准方程得答案．
【考点精析】利用圆的一般方程对题目进行判断即可得到答案，需要熟知圆的一般方程的特点：(1)①x2和y2的系数相同，不等于0．②没有xy这样的二次项；(2)圆的一般方程中有三个特定的系数D、E、F，因之只要求出这三个系数，圆的方程就确定了；(3)、与圆的标准方程相比较，它是一种特殊的二元二次方程，代数特征明显，圆的标准方程则指出了圆心坐标与半径大小，几何特征较明显．
练习册系列答案
相关题目
