题目内容
9. 用红、黄、蓝三种颜色对如图所示的三个方格进行涂色.若要求每个小方格涂一种颜色,且涂成红色的方格数为偶数,则不同的涂色方案种数是14.(用数字作答)
用红、黄、蓝三种颜色对如图所示的三个方格进行涂色.若要求每个小方格涂一种颜色,且涂成红色的方格数为偶数,则不同的涂色方案种数是14.(用数字作答)
分析 由题意可知涂成红色的方格数为0,或2,分三类,3个格涂一种颜色,3个格涂2颜色且涂0个红色时,3格涂2颜色且涂2个红色时,根据分类计数原理可得.
解答 解:因为涂成红色的方格数为偶数,即涂成红色的方格数为0,或2,
3个格涂一种颜色,有2种,(全黄或全蓝)
3个格涂2颜色且涂0个红色时,C21C32=6种,
3格涂2颜色且涂2个红色时,C21C32=6种,
根据分类计数原理,可得共有2+6+6=14种,
故答案为:14.
点评 本题考查了分类计数原理,关键是分类,属于基础题.

练习册系列答案
 双基同步导航训练系列答案
双基同步导航训练系列答案 黄冈小状元同步计算天天练系列答案
黄冈小状元同步计算天天练系列答案
相关题目
19.已知函数f(x)=10-x-|lgx|与x轴有两个交点(x1,0),(x2,0),则( )
| A. | 0<x1x2<1 | B. | x1x2=1 | C. | -1<x1x2<0 | D. | 1<x1x2<10 |
17. 从某企业生茶的某种产品中抽取100件,测量这些产品的一项质量指标值,由测量结果得如下频数分布表:
从某企业生茶的某种产品中抽取100件,测量这些产品的一项质量指标值,由测量结果得如下频数分布表:
(1)在答题卡上补全这些数据作出的频率分布直方图;
(2)估计这种产品质量指标值的平均值及方差(同一组中的数据用该组区间的中点值作代表);
(3)估计这种产品质量指标值的中位数.(精确到0.1)
 从某企业生茶的某种产品中抽取100件,测量这些产品的一项质量指标值,由测量结果得如下频数分布表:
从某企业生茶的某种产品中抽取100件,测量这些产品的一项质量指标值,由测量结果得如下频数分布表:| 质量指标值分组 | [75,85) | [85,95) | [95,105) | [105,115) | [115,125) |
| 频数 | 6 | 28 | 34 | 24 | 8 |
(2)估计这种产品质量指标值的平均值及方差(同一组中的数据用该组区间的中点值作代表);
(3)估计这种产品质量指标值的中位数.(精确到0.1)
4.设a=0.23,b=log20.3,c=20.3,则( )
| A. | b<c<a | B. | c<b<a | C. | a<b<c | D. | b<a<c |
14.如图表示的是求首项为-41,公差为2的等差数列{an}前n项和的最小值的程序框图.则①处可填写( )
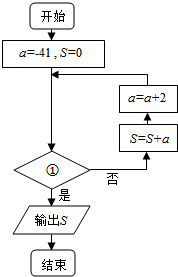

| A. | S>0 | B. | S<0 | C. | a>0 | D. | a=0 |
19.将正整数按下表排列:
则101在( )
| 第1列 | 第2列 | 第3列 | 第4列 | |
| 第1行 | 1 | 2 | 3 | 4 |
| 第2行 | 8 | 7 | 6 | 5 |
| 第3行 | 9 | 10 | 11 | 12 |
| 第4行 | 16 | 15 | 14 | 13 |
| … | … | … | … | … |
| A. | 第25行,第1列 | B. | 第25行,第4列 | C. | 第26行,第1列 | D. | 第26行,第4列 |
