题目内容
19．已知函数f（x）=10-x-|lgx|与x轴有两个交点（x1，0），（x2，0），则（ ）| A． | 0＜x1x2＜1 | B． | x1x2=1 | C． | -1＜x1x2＜0 | D． | 1＜x1x2＜10 |
分析 分别画出y=10-x（蓝色曲线）与y=|lgx|（红色曲线）的图象，如图所示，由图象可知0＜x1＜1，1＜x2＜$\frac{1}{2}$，问题得以解决．
解答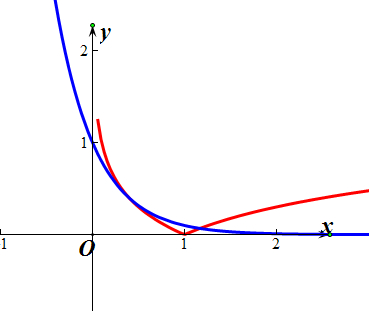 
解：分别画出y=10-x（蓝色曲线）与y=|lgx|（红色曲线）的图象，如图所示，
函数f（x）=10-x-|lgx|与x轴有两个交点（x1，0），（x2，0），
设x1＜x2，
由图象可知0＜x1＜1，1＜x2＜$\frac{1}{2}$，
∴0＜x1x2＜1，
故选：A．
点评 本题考查了函数的零点问题，以及函数的图象的画法，属于基础题．
练习册系列答案
相关题目
10．某班主任对全班50名学生进行了作业量多少的调查，数据如表：
则认为喜欢玩电脑游戏与认为作业量的多少有关系的把握大约为（ ）
附：
（K2=$\frac{n（ad-bc）2}{（a+b）（c+d）（a+c）（b+d）}$，其中n=a+b+c+d）
| 认为作业多 | 认为作业不多 | 总数 | |
| 喜欢玩电脑游戏 | 18 | 9 | 27 |
| 不喜欢玩电脑游戏 | 8 | 15 | 23 |
| 总数 | 26 | 24 | 50 |
附：
| P（K2》k0） | 0.10 | 0.05 | 0.025 | 0.010 |
| k0 | 2.706 | 3.841 | 5.024 | 6.635 |
| A． | 99% | B． | 95% | C． | 90% | D． | 无充分依据 |
7．为了解某市民众对政府出台楼市限购令的情况，在该市随机抽取了50名市民进行调查，他们月收人（单位：百元）的频数分布及对楼市限购令赞成的人数如下表：
将月收入不低于55的人称为“高收人族”，月收入低于55的人称为“非高收入族”．
（Ⅰ）根据已知条件完成下面的2x2列联表，问赞成楼市限购令与收入高低是否有关？
（Ⅱ）现从月收入在[15，25）的人中随机抽取两人，所抽取的两人都赞成楼市限购令的概率．
附：${x^2}=\frac{{n{{（{n_{11}}{n_{22}}-{n_{12}}{n_{21}}）}^2}}}{{{n_{1+}}{n_{2+}}{n_{+1}}{n_{+2}}}}，\frac{{p（{x^2}≥k）}}{k}\frac{0.050.01}{3.8416.635}$）
| 月收入 | [15，25） | [25，35） | [35，45） | [45，55） | [55，65） | [65，75） |
| 频数 | 5 | 10 | 15 | 10 | 5 | 5 |
| 赞成人数 | 4 | 8 | 12 | 5 | 2 | 1 |
（Ⅰ）根据已知条件完成下面的2x2列联表，问赞成楼市限购令与收入高低是否有关？
| 非高收入族 | 高收入族 | 总计 | |
| 赞成 | |||
| 不赞成 | |||
| 总计 |
附：${x^2}=\frac{{n{{（{n_{11}}{n_{22}}-{n_{12}}{n_{21}}）}^2}}}{{{n_{1+}}{n_{2+}}{n_{+1}}{n_{+2}}}}，\frac{{p（{x^2}≥k）}}{k}\frac{0.050.01}{3.8416.635}$）
11．已知a＜0，-1＜b＜0，那么下列不等式成立的是（ ）
| A． | a＞ab＞ab2 | B． | ab＞a＞ab2 | C． | ab＞ab2＞a | D． | ab2＞ab＞a |
用红、黄、蓝三种颜色对如图所示的三个方格进行涂色．若要求每个小方格涂一种颜色，且涂成红色的方格数为偶数，则不同的涂色方案种数是14．（用数字作答）